Penalty Functions in Optimization: Theory, Applications, and Advances for Drug Discovery

Abstract

This article provides a comprehensive overview of penalty function methods for solving constrained optimization problems, with a specialized focus on applications in drug discovery and development. It covers foundational principles, key methodological approaches including exact and quadratic penalty functions, and addresses practical challenges like parameter tuning and numerical stability. The content further explores advanced strategies for performance validation and compares penalty methods with alternative optimization frameworks, offering researchers and pharmaceutical professionals actionable insights for implementing these techniques in complex, real-world research scenarios.

Understanding Penalty Functions: Core Principles and Mathematical Foundations

What is the fundamental principle behind penalty methods?

Penalty methods are computational techniques that transform constrained optimization problems into unconstrained formulations by adding a penalty term to the objective function. This penalty term increases in value as the solution violates the problem's constraints, effectively discouraging infeasible solutions during the optimization process. The method allows researchers to leverage powerful unconstrained optimization algorithms while still honoring the original problem's constraints, either exactly or approximately.

In which research domains are penalty methods particularly valuable?

Penalty methods find extensive application in fields where constrained optimization problems naturally arise, including:

• Drug development and pharmacometrics: For computing optimal drug dosing regimens that balance efficacy and safety targets [1]
• Engineering design: For solving structural optimization problems with physical constraints
• Machine learning: For training models with specific requirements or limitations
• Optimal control theory: For solving control problems with state and control constraints [2]

Fundamental Concepts and Terminology

How do penalty methods handle different types of constraints?

The approach varies based on constraint type, as summarized in the following table:

Table 1: Penalty Method Approaches for Different Constraint Types

Constraint Type	Mathematical Form	Penalty Treatment	Example Application
Inequality	gⱼ(x) ≤ 0	Penalizes when gⱼ(x) > 0	Drug safety limits [1]
Equality	háµ¢(x) = 0	Penalizes when |háµ¢(x)| > 0	Model equilibrium conditions
State Constraints	g(y(t)) ≤ 0, t∈[t₁,t₂]	Penalizes violation over interval	Neutrophil level maintenance [1]

What key terminology should researchers understand?

• Penalty Function (P): A function that measures constraint violation, typically zero when constraints are satisfied and positive when violated [1]
• Penalty Parameter (ρ): A weighting factor that determines the relative importance of constraint satisfaction versus objective optimization [1] [3]
• Feasible Solution: A solution that satisfies all constraints of the original problem
• Infeasible Solution: A solution that violates at least one constraint
• Exact Penalty Function: A penalty function that yields the same solution as the original constrained problem for finite values of the penalty parameter

Experimental Protocols and Implementation

Basic Penalty Method Protocol

What are the systematic steps for implementing penalty methods?

• Problem Formulation: Begin by clearly defining the objective function and all constraints
• Penalty Function Selection: Choose an appropriate penalty function based on constraint types
• Parameter Initialization: Select initial penalty parameter values (typically starting with smaller values)
• Unconstrained Optimization: Solve the penalized unconstrained problem
• Parameter Update: Increase the penalty parameter according to a scheduled strategy
• Convergence Check: Verify if solution meets feasibility and optimality tolerances
• Solution Refinement: Continue iterating until satisfactory solution is obtained

Table 2: Penalty Function Types and Their Mathematical Forms

Penalty Type	Mathematical Formulation	Advantages	Limitations
Quadratic	P(x,ρ) = ρ/2 × ∑[max(0,gⱼ(x))]²	Smooth, differentiable	May require ρ→∞ for exactness
ℓ₁-Exact	P(x,ρ) = ρ × ∑|hᵢ(x)| + ρ × ∑max(0,gⱼ(x))	Finite parameter suffices	Non-differentiable at constraints
Exponential	P(x,ρ) = ∑exp(ρ×gⱼ(x))	Very smooth	Can become numerically unstable
Objective Penalty	F(x,M) = Q(f(x)-M) + ∑P(gⱼ(x))	Contains objective penalty factor M [4]	More complex implementation

Advanced Protocol: State-Constrained Optimal Control

How are penalty methods implemented for dynamic systems with state constraints?

For pharmacometric applications involving dynamic systems, researchers can implement the enhanced OptiDose protocol [1]:

• Define the Pharmacometric Model: Formulate the system dynamics using ordinary differential equations: dy/dt = f(t,y(t),θ,D), y(tâ‚€) = yâ‚€(θ) where y represents model states, θ denotes parameters, and D represents doses [1]

• Specify Therapeutic Targets: Define efficacy and safety targets mathematically:

  • Efficacy: Typically expressed through cost function J(D) = ∫W(t,D)dt
  • Safety: Usually formulated as state constraints N(t,D) ≥ threshold [1]

• Formulate State-Constrained Optimal Control Problem: min J(D) subject to state constraints and bounds on D [1]

• Apply Penalty Transformation: Convert to unconstrained problem using: min J(D) + P(D,ρ) where P(D,ρ) = ρ/2 × ∫[max(0,1-N(t,D))]²dt [1]

• Implement in Software: Utilize pharmacometric software like NONMEM for solution

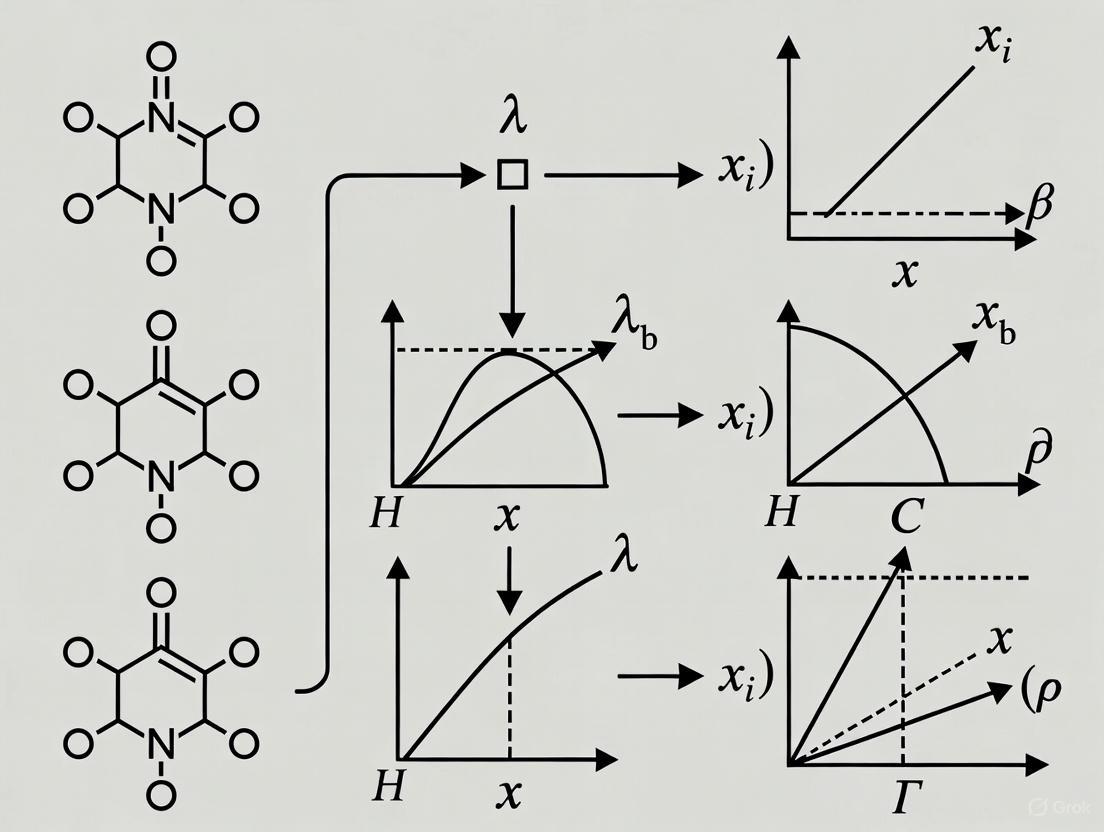
Diagram 1: Penalty Method Transformation Workflow (76 characters)

Troubleshooting Common Implementation Issues

Parameter Selection Problems

How should researchers select appropriate penalty parameters?

Table 3: Penalty Parameter Selection Guidelines

Problem Type	Initial Value	Update Strategy	Convergence Criteria
Inequality Constraints	ρ₀ = 1-10	ρₖ₊₁ = 10×ρₖ	max(gⱼ(x)) ≤ ε₁
Equality Constraints	ρ₀ = 10-100	ρₖ₊₁ = 5×ρₖ	|hᵢ(x)| ≤ ε₂
Mixed Constraints	ρ₀ = 10-50	Adaptive based on violation	Combined tolerance

What should I do if my solution remains infeasible despite high penalty parameters?

This common issue typically stems from:

• Insufficient penalty parameter magnitude: Systematically increase ρ until feasibility is achieved
• Numerical precision limitations: Implement exact penalty functions or smoothing techniques [5]
• Ill-conditioning: Use augmented Lagrangian methods for better conditioning
• Local minima: Employ global optimization strategies or multi-start approaches

Numerical Stability Issues

Why does my optimization fail when using very large penalty parameters?

Large penalty parameters create ill-conditioned optimization landscapes that challenge numerical algorithms. Address this by:

• Implementing smoothing techniques: Replace non-differentiable functions with smoothed approximations [5]
• Using exact penalty methods: These methods yield exact solutions for finite penalty parameters
• Applying homotopy methods: Gradually increase penalty parameters while using previous solutions as initial guesses
• Switching to specialized algorithms: Use methods specifically designed for penalized formulations

Research Reagent Solutions

Table 4: Essential Computational Tools for Penalty Method Implementation

Tool Category	Specific Examples	Primary Function	Application Context
Optimization Software	NONMEM, MATLAB, Python SciPy	Solve unconstrained optimization problems	Pharmacometrics, general research [1]
Penalty Function Libraries	Custom implementations in C++, Python	Provide pre-coded penalty functions	Algorithm development
Modeling Environments	R, Julia, Python Pyomo	Formulate and manipulate optimization models	Prototyping and analysis
Differential Equation Solvers	SUNDIALS, LSODA, ode45	Solve system dynamics in optimal control	Pharmacokinetic-pharmacodynamic models [1]

Applications in Drug Development and Pharmacometrics

How are penalty methods applied to optimize drug dosing regimens?

In pharmacometrics, penalty methods enable computation of optimal drug doses that balance efficacy and safety:

• Define Dosing Scenario: Fix dosing times and optimize dose amounts D = (D₁,Dâ‚‚,...,Dₘ) [1]
• Formulate Efficacy Target: Typically expressed as minimizing a cost function, e.g., J(D) = ∫TumorWeight(t,D)dt [1]
• Implement Safety Constraints: Represented as state constraints, e.g., N(t,D) ≥ 1 [1]
• Apply Penalty Transformation: Convert to unconstrained problem using penalty functions
• Compute Optimal Doses: Solve using appropriate optimization algorithms

What specific challenges arise when applying penalty methods to pharmacometric problems?

• Model complexity: Pharmacometric models often involve complex nonlinear dynamics
• Multiple constraints: Simultaneous handling of efficacy, safety, and practical constraints
• Parameter uncertainty: Model parameters may be estimated with significant uncertainty
• Clinical feasibility: Solutions must be practically implementable in clinical settings

Advanced Techniques and Recent Developments

What recent advancements address traditional penalty method limitations?

Recent research has developed enhanced penalty approaches:

• Smoothing ℓ₁-Exact Penalty Methods: Combine the exactness of ℓ₁ penalties with improved differentiability through smoothing techniques [5]
• Objective Filled Penalty Functions: Enable global optimization by systematically exploring better local minima [4]
• Adaptive Penalty Methods: Dynamically adjust penalty parameters based on convergence behavior
• Exponential Penalty Functions: Provide alternative formulations for optimal control problems [2]

Diagram 2: Penalty Method Iterative Algorithm (76 characters)

Frequently Asked Questions (FAQs)

What is the fundamental difference between penalty and barrier methods?

Penalty methods allow constraint violation during optimization but penalize it in the objective function, while barrier methods prevent constraint violation entirely by creating a "barrier" at the constraint boundary. Penalty methods can handle both equality and inequality constraints, while barrier methods are primarily for inequality constraints.

How do I know if my penalty function is working correctly?

Monitor these indicators during optimization:

• Consistent decrease in both objective function and constraint violation
• Progressive approach toward feasibility
• Stable convergence behavior
• Reasonable computation time

When should I use penalty methods instead of other constrained optimization approaches?

Penalty methods are particularly advantageous when:

• You have efficient unconstrained optimization algorithms available
• The problem has complex constraints that are difficult to handle directly
• You need to solve optimal control problems with state constraints [1]
• You're working with existing software that primarily supports unconstrained optimization

Can penalty methods guarantee global optimality for non-convex problems?

Traditional penalty methods cannot guarantee global optimality for non-convex problems. However, filled penalty functions [4] specifically address this limitation by helping escape local minima and continue searching for better solutions, potentially leading to global or near-global optima.

Foundational Concepts: FAQs on Penalty Methods and Constraint Violation

FAQ 1: What is a penalty function in the context of constrained optimization?

A penalty function is an algorithmic tool that transforms a constrained optimization problem into a series of unconstrained problems. This is achieved by adding a penalty term to the original objective function; this term consists of a penalty parameter multiplied by a measure of how much the constraints are violated. The solution to these unconstrained problems ideally converges to the solution of the original constrained problem [6].

FAQ 2: How is "constraint violation" quantitatively measured?

Constraint violation is measured using functions that are zero when constraints are satisfied and positive when they are violated. A common measure for an inequality constraint ( gj(x) \leq 0 ) is ( \max(0, gj(x)) ). The overall violation is often the sum of these measures for all constraints. For example, a quadratic penalty function uses ( \sum g( ci(x) ) ) where ( g(ci(x)) = \max(0, c_i(x))^2 ) [6]. In evolutionary algorithms and other direct methods, the Overall Constraint Violation (CV) is frequently calculated as the sum of the absolute values of the violation for each constraint [7].

FAQ 3: What is the difference between exterior and interior penalty methods?

The key difference lies in the approach to the feasible region and the behavior of the penalty parameter.

• Exterior Penalty Methods: These methods start from infeasible points (outside the feasible region). The penalty parameter is increased over iterations, drawing the solution toward feasibility from the outside. They are generally more robust [8].
• Interior Penalty (Barrier) Methods: These methods start from a feasible point and prevent the solution from leaving the feasible region. The penalty parameter is decreased to zero, allowing the solution to approach the boundary from the inside [6] [8].

FAQ 4: My penalty parameter is becoming very large, leading to numerical instability and slow convergence. What are my options?

This ill-conditioning is a known disadvantage of classic penalty methods [6]. Consider these alternatives:

• Augmented Lagrangian Method (ALM): This method incorporates Lagrange multiplier estimates in addition to the penalty parameter. This allows for convergence to the true solution without the penalty parameter going to infinity, thus avoiding much of the ill-conditioning [6].
• Filled Penalty Functions: For global optimization, advanced penalty functions with "filling" properties can help escape local optima without relying solely on an infinite penalty parameter [4].

FAQ 5: How do I handle uncertain constraints where parameters are not known precisely?

For problems with interval-valued uncertainties, a novel approach is to define an Interval Constraint Violation (ICV). This method classifies solutions as feasible, infeasible, or partially feasible based on the bounds of the uncertain constraints. A two-stage penalty function can then be applied, which tends to retain superior partially feasible and infeasible solutions in the early stages of evolution to promote exploration [9].

A Taxonomy of Penalty Functions: Measuring Violation

The following table summarizes common penalty functions and how they measure constraint violation.

Table 1: Common Penalty Functions and Their Properties

Penalty Function Type	Mathematical Formulation (for min f(x) s.t. g_j(x) ≤ 0)	Measure of Violation	Key Characteristics
Quadratic Penalty [6]	( f(x) + p \sum \max(0, g_j(x))^2 )	Squared violation	Exterior method. Simple, but requires ( p \to \infty ).
Log Barrier [8]	( f(x) - r \sum \log(-g_j(x)) )	Logarithmic of constraint value	Interior method. Requires initial feasible point. ( r \to 0 ).
Inverse Barrier [8]	( f(x) + r \sum \frac{-1}{g_j(x)} )	Inverse of constraint value	Interior method. Requires initial feasible point. ( r \to 0 ).
Objective Penalty [4]	( Q(f(x) - M) + \rho \sum P(g_j(x)) )	Separate functions ( Q ) and ( P ) for objective and constraints	Uses an objective penalty factor ( M ) in addition to a constraint penalty factor ( \rho ).
Filled Penalty [4]	( H{\varepsilon}(x, \overline{x}, M, \rho) = Q(f(x)-M) + \rho \sum p{\varepsilon}(gj(x)) + \rho p{\varepsilon}(f(x)-f(\overline{x})+2\varepsilon) )	Composite measure including distance from current local solution ( \overline{x} )	Designed for global optimization. Helps escape local optima by "filling" them.

Troubleshooting Common Experimental Issues

Issue: Algorithm Converges to an Infeasible Solution

• Potential Cause 1: The penalty parameter is not large enough to enforce constraint satisfaction.
• Solution: For exterior methods, systematically increase the penalty parameter ( p ) or ( \rho ) according to a schedule (e.g., multiply by 10 each iteration) [6] [8].
• Potential Cause 2: The algorithm is trapped in a local optimum of the penalized function.
• Solution: Consider using a filled penalty function that adds a term to help the search escape the basin of attraction of the current local solution [4].

Issue: Slow Convergence or Numerical Instability

• Potential Cause: The penalty parameter has become very large, making the Hessian of the penalized function ill-conditioned.
• Solution: Switch to the Augmented Lagrangian Method, which avoids the need for the penalty parameter to go to infinity [6]. Alternatively, use a more sophisticated unconstrained optimizer that can handle poor conditioning.

Issue: Handling a Mix of Relaxable and Unrelaxable Constraints

• Explanation: Unrelaxable constraints (e.g., physical laws) must be satisfied for a solution to be meaningful, while relaxable constraints (e.g., performance targets) can be slightly violated [7].
• Solution: Use a hybrid strategy. Apply an extreme barrier approach for unrelaxable constraints (assigning an infinite penalty if violated) and a standard penalty function for relaxable constraints. This prevents the waste of computational resources on physically meaningless solutions [7].

Experimental Protocol: Implementing a Quadratic Penalty Method

This protocol provides a step-by-step guide for solving a constrained optimization problem using a basic quadratic exterior penalty method.

Objective: Minimize ( f(x) ) subject to ( g_j(x) \leq 0, j \in J ).

Materials & Reagents: Table 2: Research Reagent Solutions for Penalty Method Experiments

Item	Function in the Experiment
Unconstrained Optimization Solver (e.g., BFGS, Gradient Descent)	The core computational engine for minimizing the penalized objective function at each iteration.
Initial Penalty Parameter (( p_0 ))	A positive scalar value to initialize the penalty process.
Penalty Increase Factor (( \beta ))	A multiplier (e.g., 10) to increase the penalty parameter each iteration.
Convergence Tolerance (( \epsilon ))	A small positive scalar to determine when to stop the iterations.

Methodology:

• Initialization: Choose an initial guess ( x^0 ), an initial penalty parameter ( p_0 > 0 ), a penalty increase factor ( \beta > 1 ), and a convergence tolerance ( \epsilon > 0 ). Set ( k = 0 ).
• Formulate Penalized Objective: Construct the quadratic penalized function: ( Q(x; pk) = f(x) + pk \sum{j \in J} \max(0, gj(x))^2 ) [6].
• Solve Unconstrained Subproblem: Using the unconstrained optimization solver, find an approximate minimizer of ( Q(x; p_k) ), starting from ( x^k ). Denote the solution as ( x^{k+1} ).
• Check for Convergence: Evaluate the maximum constraint violation: ( \text{violation} = \maxj \max(0, gj(x^{k+1})) ). If ( \text{violation} < \epsilon ), stop and output ( x^{k+1} ) as the solution.
• Update Parameters: Increase the penalty parameter: ( p{k+1} = \beta pk ). Set ( k = k + 1 ) and return to Step 2.

Diagram 1: Quadratic Penalty Method Workflow

Advanced Methodologies: Filled Penalty Functions for Global Optimization

For non-convex problems with multiple local minima, standard penalty methods may converge to a local solution. Filled penalty functions are designed to help find the global optimum.

Concept: A filled penalty function modifies the objective landscape not only by penalizing constraint violation but also by "filling" the basin of attraction of a local solution that has already been found. This allows the search algorithm to proceed to a potentially better local solution [4].

Experimental Workflow: The following diagram illustrates a typical algorithm using a filled penalty function to escape a local optimum and continue the search for a global one.

Diagram 2: Filled Penalty Global Search

Frequently Asked Questions (FAQs)

Q1: What is the fundamental concept behind a penalty method in constrained optimization?

Penalty methods are a class of algorithms that transform a constrained optimization problem into a series of unconstrained problems. This is achieved by adding a term, known as a penalty function, to the original objective function. This term consists of a penalty parameter multiplied by a measure of how much the constraints are violated. The measure is zero when constraints are satisfied and becomes nonzero when they are violated. Ideally, the solutions to these unconstrained problems converge to the solution of the original constrained problem [6].

Q2: What are the common types of penalty functions used in practice?

The two most common penalty functions in constrained optimization are the quadratic penalty function and the deadzone-linear penalty function [6]. Furthermore, the Lq penalty, a generalization that includes both L1 (linear) and L2 (quadratic) penalties, is used in advanced applications like clinical drug response prediction for its variable selection properties [10].

Q3: What is a major practical disadvantage of the penalty method?

A significant disadvantage is that as the penalty coefficient p is increased to enforce constraint satisfaction, the resulting unconstrained problem can become ill-conditioned. This means the coefficients in the problem become very large, which may cause numeric errors and slow down the convergence of the unconstrained minimization algorithm [6].

Q4: What are the alternatives if my optimization fails due to the ill-conditioning of penalty methods?

Two prominent alternative classes of algorithms are:

• Barrier Methods: These keep the iterates within the interior of the feasible domain and use a barrier to bias them away from the boundary. They are often more efficient than simple penalty methods [6].
• Augmented Lagrangian Methods: These are advanced penalty methods that allow for high-accuracy solutions without needing to drive the penalty coefficient to infinity, thereby avoiding the ill-conditioning issue and making the problems easier to solve [6].

Troubleshooting Guide

Issue 1: Poor Convergence or Numerical Errors

• Problem: The optimization algorithm converges very slowly, fails to converge, or produces NaN/Inf values. The solution seems to oscillate or diverge as the penalty parameter increases.
• Cause: This is a classic symptom of an ill-conditioned problem, which occurs when using a simple penalty method and making the penalty parameter too large [6].
• Solution:
  • Switch Methods: Consider using an Augmented Lagrangian Method instead of a basic penalty method. These methods are designed to avoid the ill-conditioning problem [6].
  • Use a Sequence: If you must use a basic penalty method, implement a gradual increase of the penalty parameter. Do not start with an extremely large value. Solve the unconstrained problem for a moderate p, then use that solution as the initial guess for a new problem with a larger p.
  • Robust Estimators: If your objective function or constraints are based on statistical models (e.g., in drug response prediction), consider using robust estimators (like MM-estimators) for parameters. These are less influenced by outliers, which can stabilize the optimization process [11].

Issue 2: Choosing the Right Penalty Constant

• Problem: The final solution is highly sensitive to the choice of the penalty constant, and there is no clear rule for selecting an appropriate value.
• Cause: A key drawback of some penalty methods, like the Penalty Function (PM) approach in dual response surface optimization, is the lack of a systematic rule for determining the penalty constant, leaving it to subjective judgment [11].
• Solution:
  • Incorporate Decision Maker's Preference: Implement a systematic method like the Penalty Function Method based on the Decision Maker's (DM) preference structure (PMDM). This technique provides a structured way to determine the penalty constant ξ by formally incorporating the priorities of the decision maker, such as the relative importance of meeting a target mean versus minimizing variance [11].
  • Cross-Validation: For data-driven problems, use techniques like cross-validation to evaluate the performance of different penalty constants on a validation dataset and select the one that provides the best, most stable performance.

Issue 3: Inaccurate Solution - Constraint Violation

• Problem: The optimization completes, but the solution violates one or more constraints beyond an acceptable tolerance.
• Cause: The penalty parameter is not large enough to sufficiently penalize the constraint violations, or the optimization was stopped before fully converging [6].
• Solution:
  • Increase Penalty Parameter: Systematically increase the penalty parameter and re-run the optimization, using the previous solution as an initial guess.
  • Use an Exact Penalty Function: Consider switching to an L1 (linear) exact penalty function. For a sufficiently large (but finite) penalty parameter, an exact penalty function can recover the exact solution to the constrained problem, whereas quadratic penalties only satisfy constraints in the limit as the parameter goes to infinity.
  • Check Convergence Criteria: Tighten the convergence tolerances for the unconstrained solver to ensure it finds a true minimum for the penalized function.

Comparison of Common Penalty Functions

The table below summarizes the key characteristics of the three primary penalty forms discussed.

Penalty Function	Mathematical Form (for constraint c(x) ≤ 0)	Key Advantages	Key Disadvantages / Troubleshooting Notes
Quadratic (L2)	( g(c(x)) = \max(0, c(x))^2 ) [6]	Smooth function, works well with gradient-based optimizers.	Not exact; can cause ill-conditioning with large p [6].
Linear (L1)	( g(c(x)) = \max(0, c(x)) )	An "exact" penalty function; constraints can be satisfied exactly for a finite p.	Non-smooth at the boundary, which can challenge some optimizers.
Exact Penalty	Combines L1 penalty for constraints with a finite parameter.	Exact solution for finite penalty parameter; avoids ill-conditioning.	Requires careful selection of the single, finite penalty parameter.

Experimental Protocol: Systematic Penalty Constant Determination

This protocol outlines the methodology for determining an effective penalty constant using the PMDM approach, as applied in dual response surface optimization [11].

• Problem Formulation:

  • Define your primary objective function (e.g., process mean, (\hat{\mu}(x))) and standard deviation function ((\hat{\sigma}(x))).
  • Set the target value, (T), for the primary objective.

• Define Decision Maker's Preference:

  • Elicit from the decision maker the acceptable trade-off between bias (deviation from target) and variance. For example, determine the maximum allowable bias, (\delta).
  • This preference structure is formalized into a rule for calculating the penalty constant (\xi). An example rule is (\xi = \frac{w}{|\hat{\mu}(x0) - T|}), where (w) is a weight reflecting the DM's preference and (x0) is a starting design point [11].

• Robust Parameter Estimation (Optional but Recommended):

  • To protect against outliers in experimental data, use robust estimators (e.g., MM-estimators) instead of Ordinary Least Squares (OLS) to fit the models for (\hat{\mu}(x)) and (\hat{\sigma}(x)) [11].

• Optimization Loop:

  • Construct the penalized objective function: ( F(x) = \hat{\sigma}(x) + \xi \cdot |\hat{\mu}(x) - T| ).
  • Use a suitable unconstrained optimization algorithm to minimize (F(x)).
  • Validate the solution by checking that the bias (|\hat{\mu}(x^*) - T|) is within the acceptable limit (\delta).

Workflow Visualization

The following diagram illustrates the logical workflow and decision points for selecting and troubleshooting penalty methods.

The Scientist's Toolkit: Research Reagent Solutions

The table below details key computational and methodological "reagents" essential for experiments in penalty-based optimization.

Item / Technique	Function / Role in Experiment	Key Consideration
Quadratic Penalty Function	Smoothly penalizes squared constraint violation, enabling use of gradient-based solvers.	Prone to ill-conditioning; requires a sequence of increasing penalty parameters [6].
L1 Penalty Function	Penalizes constraint violation linearly; forms the basis for exact penalty methods.	Non-smoothness requires specialized optimizers; choice of penalty constant is critical.
MM-Estimators	Robust statistical estimators used to fit model parameters from data, reducing the influence of outliers [11].	Protects the optimization process from being skewed by anomalous data points.
Decision Maker (DM) Preference Elicitation	A systematic procedure to formally capture trade-off preferences (e.g., bias vs. variance) to determine parameters like ξ [11].	Moves the penalty constant selection from an ad-hoc process to a structured, justifiable one.
Cross-Validation	A model validation technique used to assess how the results of a statistical analysis will generalize to an independent data set.	Useful for empirically tuning the penalty constant to avoid overfitting.

Frequently Asked Questions

FAQ 1: Why does my penalty method converge very slowly, or not at all, to a feasible solution?

• Answer: Slow convergence to a feasible solution is often due to the ill-conditioning of the unconstrained problem as the penalty parameter p becomes very large [6]. As p increases, the algorithm struggles to make progress because the Hessian of the penalized objective function becomes ill-conditioned, leading to numerical errors and slow convergence [6]. To troubleshoot:
  • Verify Constraint Violation Calculation: Ensure the measure of violation g(c_i(x)) is correctly implemented. For inequality constraints, this is typically max(0, c_i(x))^2 [6].
  • Adjust Penalty Increase Rate: Avoid increasing the penalty parameter p too aggressively. Use a gradual update scheme (e.g., p_{k+1} = β * p_k where β is a small constant like 2 or 5) to prevent immediate ill-conditioning.
  • Consider Algorithm Switch: For high-accuracy solutions, consider switching to an Augmented Lagrangian Method, which avoids the need to make p go to infinity and is less prone to ill-conditioning [6].

FAQ 2: Under what theoretical conditions can I guarantee convergence for a penalty method?

• Answer: Convergence guarantees rely on specific theoretical conditions [6]:
  • For global optimizers: If the objective function f has bounded level sets and the original constrained problem is feasible, then as the penalty coefficient p increases, the solutions of the penalized unconstrained problems will converge to the global solution of the original problem [6]. This is particularly helpful when the penalized objective function f_p is convex.
  • For local optimizers: If a local optimizer x* of the original problem is non-degenerate, there exists a neighborhood around it and a sufficiently large p_0 such that for all p > p_0, the penalized objective will have a single critical point in that neighborhood that approaches x* [6]. A "non-degenerate" point means the gradients of the active constraints are linearly independent and second-order sufficient optimality conditions are satisfied.

FAQ 3: What is the expected convergence rate for a modern penalty method on nonconvex problems?

• Answer: For complex nonconvex problems with nonlinear constraints, the convergence rate can be characterized by the number of iterations required to find an ε-approximate first-order stationary point. Recent research on linearized â„“_q penalty methods has established a convergence rate of O(1/ε^{2+ (q-1)/q}) outer iterations to reach an ε-first-order solution, where q is a parameter in (1, 2] that defines the penalty norm [12]. This provides a theoretical upper bound on the algorithm's complexity.

FAQ 4: How do I verify that the solution found by a penalty method satisfies optimality conditions?

• Answer: To verify optimality, you must check the Karush-Kuhn-Tucker (KKT) conditions at the proposed solution. The solution from the penalty method approximates the true KKT point. Your verification should include:
  • Primal Feasibility: Check that c_i(x) ≤ 0 for all constraints i ∈ I within a small tolerance.
  • Dual Feasibility: Verify that the Lagrange multipliers (λ_i) for the constraints are non-negative. These are often estimated by λ_i ≈ 2 * p * max(0, c_i(x)) for a quadratic penalty.
  • Stationarity: Check that the gradient of the Lagrangian, ∇f(x) + Σ λ_i ∇c_i(x), is approximately zero.
  • Complementary Slackness: Verify that λ_i * c_i(x) ≈ 0 for all i.

Convergence Analysis Data

Table 1: Comparison of Penalty Method Convergence Properties

Method / Aspect	Theoretical Convergence Guarantee	Theoretical Convergence Rate	Key Assumptions
Classical Quadratic Penalty	To global optimum [6]	Not specified in results	Bounded level sets, feasible original problem, convex penalized objective [6]
Linearized ℓ_q Penalty [12]	To an ε-first-order solution [12]	O(1/ε^{2+ (q-1)/q}) outer iterations [12]	Locally smooth objective and constraints, nonlinear equality constraints [12]

Table 2: Troubleshooting Common Convergence Issues

Problem Symptom	Potential Causes	Recommended Solution
Slow convergence to feasibility	Ill-conditioning from large penalty parameter p [6]	Use a more gradual schedule for increasing p; switch to Augmented Lagrangian method [6]
Convergence to an infeasible point	Penalty parameter p is too small [6]	Increase p and restart optimization; check constraint violation implementation [6]
Numerical errors (overflow, NaN)	Extremely large values in the penalized objective or its gradient due to high p [6]	Use a safeguarded optimization algorithm; re-scale the problem; employ a more numerically stable penalty function

Experimental Protocols

Protocol 1: Implementing and Testing a Basic Quadratic Penalty Method

This protocol provides a step-by-step methodology for solving a constrained optimization problem using a quadratic penalty method.

• Problem Formulation: Begin with a constrained problem: min_x f(x) subject to c_i(x) ≤ 0.
• Penalized Objective Construction: Formulate the unconstrained penalized objective: min_x f_p(x) = f(x) + p * Σ_i ( max(0, c_i(x)) )^2.
• Optimization Loop: a. Initialize: Choose an initial guess x_0, an initial penalty parameter p_0 > 0, and a scaling factor β > 1. b. Solve Unconstrained Problem: For the current p_k, use an unconstrained optimization algorithm (e.g., BFGS, Newton's method) to find x*(p_k) that minimizes f_p(x). c. Check Convergence: If the constraint violation max_i |max(0, c_i(x))| is below a predefined tolerance, stop. The solution is found. d. Increase Penalty: Set p_{k+1} = β * p_k. e. Update Initial Guess: Use x*(p_k) as the initial guess for the next iteration with p_{k+1}. f. Iterate: Repeat steps (b) to (e) until convergence.

Protocol 2: Numerical Verification of Convergence Guarantees

This protocol outlines how to empirically test the theoretical convergence of a penalty method, aligning with frameworks used in theoretical analysis [13].

• Synthetic Problem Setup: Generate a set of test problems with known optimal solutions x* and known optimal values f(x*). This allows for calculating the exact error.
• Metric Definition: Define the metrics to track:
  • Distance to Optimum: ||x_k - x*||
  • Objective Error: |f(x_k) - f(x*)|
  • Constraint Violation: max_i |max(0, c_i(x_k))|
• Algorithm Execution: Run the penalty method from Protocol 1 on the test problems, recording the defined metrics at each outer iteration k.
• Rate Calculation: Plot the metrics (e.g., Constraint Violation) against the iteration count k on a log-log scale. The slope of the line in the limiting regime gives an empirical estimate of the convergence rate, which can be compared to theoretical bounds like O(1/ε^{2+ (q-1)/q}) [12].

Workflow and Relationship Visualizations

The Scientist's Toolkit

Table 3: Key Research Reagent Solutions for Penalty Method Experiments

Item / Concept	Function in the "Experiment"
Penalty Parameter (p)	Controls the weight of the constraint violation penalty. A sequence of increasing p values drives the solution towards feasibility [6].
Penalty Function (g(c_i(x)))	A measure of constraint violation, typically max(0, c_i(x))^2 for inequalities. It transforms the constrained problem into an unconstrained one [6].
Unconstrained Solver	The algorithm (e.g., BFGS, Gradient Descent) used to minimize the penalized objective f_p(x) for a fixed p [6].
ℓ_q Norm (for q ∈ (1,2])	Used in modern penalty methods to define the penalty term. The parameter q offers a trade-off, influencing the sparsity and the theoretical convergence rate [12].
Quadratic Regularization	A term added to the subproblem in linearized methods to ensure boundedness and improve numerical stability, often controlled by a dynamic rule [12].

Frequently Asked Questions

Q1: My penalized objective function is becoming ill-conditioned as I increase the penalty parameter, leading to slow convergence or numerical errors. What can I do? This is a common issue because large penalty parameters create very steep "walls" around the feasible region, making the Hessian of the objective function ill-conditioned [6]. To mitigate this:

• Use a Gradual Approach: Instead of starting with a very large p, solve a sequence of unconstrained problems where you gradually increase p from a small value. This allows the optimization algorithm to use the solution from the previous p as a warm start for the next, more difficult problem.
• Consider Alternative Methods: For high-accuracy solutions, Augmented Lagrangian Methods are often preferred as they can achieve convergence without needing to drive the penalty coefficient to infinity, thus avoiding much of the ill-conditioning [6].

Q2: How do I know if my penalty parameter is large enough to enforce the constraints effectively? A sufficiently large penalty parameter will result in a solution that satisfies the constraints within a desired tolerance. Monitor the constraint violation c_i(x) during your optimization. If the final solution still significantly violates constraints, you need to increase p. Theoretically, the solution of the penalized problem converges to the solution of the original constrained problem as p approaches infinity [6]. In practice, you should increase p until the constraint violations fall below your pre-defined threshold.

Q3: Are there modern penalty methods that perform better for complex, non-convex problems like those in machine learning? Yes, recent research has developed more sophisticated penalty methods. For example, the smoothing L1-exact penalty method has been proposed for challenging problems on Riemannian manifolds. This method combines the exactness of the L1-penalty (which can yield exact solutions for a finite p) with a smoothing technique to make the problem easier to solve [5]. Such advances are particularly relevant for enforcing fairness, safety, and other requirements in machine learning models [14].

Troubleshooting Guides

Problem: Slow Convergence of the Unconstrained Solver

• Symptoms: The optimization algorithm takes many iterations to converge when minimizing f_p(x), especially for larger values of p.
• Potential Causes:
  • Ill-conditioned Problem: As p grows, the condition number of the Hessian of f_p(x) worsens, slowing down gradient-based methods [6].
  • Poor Starting Point: Starting with a very large p from the beginning can trap the solver in a region of poor performance.
• Solutions:
  • Implement a Continuation Strategy: As outlined in FAQ 1, increase p gradually.
  • Switch to a Robust Solver: Use unconstrained optimization methods that are designed to handle ill-conditioned problems effectively.
  • Explore Exact Penalty Formulations: Methods like the L1-exact penalty can sometimes avoid the need for p to go to infinity, thus mitigating the ill-conditioning issue [5].

Problem: Infeasible Final Solution

• Symptoms: The optimization run completes, but the solution x* does not satisfy the constraints c_i(x*) ≤ 0 to the required precision.
• Potential Causes:
  • Insufficient Penalty Parameter: The value of p is not large enough to strongly penalize constraint violations.
  • Conflict Between Objective and Constraints: The objective function f(x) may pull the solution strongly towards a region that is infeasible.
• Solutions:
  • Increase p Systematically: Re-run the optimization with a larger penalty parameter. You may need to do this several times.
  • Verify Problem Formulation: Double-check that your constraints are realistic and feasible. There may be a fundamental conflict in your problem setup.

Experimental Protocol for Penalty Method Tuning

This protocol provides a step-by-step methodology for empirically determining a suitable penalty parameter sequence.

1. Objective and Constraint Definition

• Define your objective function f(x) and constraints c_i(x) ≤ 0.
• Formulate the penalized objective: f_p(x) = f(x) + p * Σ_i g(c_i(x)), where a common choice for g is the quadratic penalty function: g(c_i(x)) = [max(0, c_i(x))]^2 [6].

2. Parameter Selection Experiment

• Setup: Choose a geometrically increasing sequence of penalty parameters (e.g., p = 1, 10, 100, 1000, ...).
• Procedure: For each value of p in the sequence:
  • Minimize: Use an unconstrained optimization algorithm to find x*(p) that minimizes f_p(x).
  • Warm Start: Use the solution x*(p_prev) from the previous, smaller p as the initial guess for the next, larger p.
  • Record: For each run, record the final objective f(x*(p)), the maximum constraint violation max_i c_i(x*(p)), and the number of iterations required for convergence.

3. Analysis and Interpretation

• Create a summary table of the quantitative results from your experiment:

Penalty Parameter (p)	Final Objective f(x*)	Max Constraint Violation	Iterations to Convergence
1
10
100
1000

• Interpretation: A well-chosen sequence will show the constraint violation decreasing to an acceptable level while the objective value f(x*) stabilizes. A sharp increase in iterations indicates the problem is becoming ill-conditioned.

The Scientist's Toolkit: Research Reagent Solutions

Item	Function in Penalty Method Research
Quadratic Penalty Function	A differentiable penalty term, [max(0, c_i(x))]^2, suitable for use with gradient-based optimizers. It penalizes violations more severely as they increase [6].
L1-Exact Penalty Function	A non-differentiable but "exact" penalty function, `Σ_i	c_i(x)	, meaning it can recover the exact solution of the constrained problem for a finite value ofpwithout needingp→∞` [5].
Smoothing Functions	Used to create differentiable approximations of non-differentiable functions (like the L1-penalty), enabling the use of standard gradient-based solvers [5].
Extended Mangasarian-Fromovitz Constraint Qualification (EMFCQ)	A theoretical tool used to prove the boundedness of Lagrange multipliers and the global convergence of penalty methods to feasible and optimal solutions [5].

Penalty Method Workflow Visualization

Diagram 1: The iterative process of the penalty method, showing how the penalty parameter is updated until constraints are satisfied.

Penalty Parameter Selection Strategy

Diagram 2: The trade-off in selecting the penalty parameter and the recommended strategy to balance it.

Implementing Penalty Methods: Techniques and Drug Discovery Case Studies

Core Concepts and Definitions

What is the fundamental principle behind Sequential Unconstrained Minimization Techniques (SUMT)?

Sequential Unconstrained Minimization Techniques (SUMT) are a class of algorithms for solving constrained optimization problems by converting them into a sequence of unconstrained problems [6]. The core principle involves adding a penalty term to the original objective function; this term penalizes constraint violations [3] [6]. A parameter controls the severity of the penalty, which is progressively increased across the sequence of problems, forcing the solution towards feasibility in the original constrained problem [6].

How do penalty methods relate to SUMT and what are their primary components?

Penalty methods are the foundation of SUMT [6]. The modified, unconstrained objective function takes the form: fp(x) := f(x) + p * Σ g(ci(x)) [6].

• f(x): The original objective function to be minimized [6].
• Penalty Function (g(ci(x))): A function that measures the violation of the constraints. A common choice for inequality constraints is the quadratic penalty: g(ci(x)) = max(0, ci(x))^2 [6].
• Penalty Parameter (p): A positive coefficient that is sequentially increased. A larger p imposes a heavier cost for constraint violations [3] [6].

What are the main theoretical guarantees for the convergence of penalty methods?

Theoretical results ensure that under certain conditions, the solutions to the penalized unconstrained problems converge to the solution of the original constrained problem [6].

• For bounded objective functions and a feasible original problem, the set of global optimizers of the penalized problem will eventually reside within an arbitrarily small neighborhood of the global optimizers of the original problem as p increases [6].
• For a non-degenerate local optimizer of the original problem, there exists a neighborhood and a sufficiently large p0 such that for all p > p0, the penalized objective has exactly one critical point in that neighborhood, which converges to the original local optimizer [6].

Troubleshooting Guides and FAQs

Algorithm Configuration and Parameter Tuning

FAQ: How do I select an appropriate initial penalty parameter p and a strategy for increasing it?

Choosing the initial penalty parameter is a common challenge. If p is too small, the algorithm may venture too far into infeasible regions. If it is too large, the unconstrained problem becomes ill-conditioned early on, leading to slow convergence or numerical errors [3] [6].

• Problem: Poor convergence due to incorrect initial penalty parameter.
• Solution: Start with a moderate p0 (e.g., 1.0 or 10.0) and use a multiplicative update rule (e.g., p_{k+1} = β * p_k, with β in [2, 10]) [6]. Monitor the constraint violation; if it remains high, increase β.
• Solution: Implement a strategy that only increases p if the reduction in constraint violation from the previous iteration is below a certain threshold.

FAQ: My algorithm is converging slowly. What might be the cause?

Slow convergence in SUMT can stem from several factors, primarily related to the penalty function and the solving of the unconstrained subproblems.

• Problem: Ill-conditioning of the unconstrained subproblem due to a very large penalty parameter p [6].
• Solution: Instead of a simple penalty method, consider an Augmented Lagrangian Method, which incorporates a Lagrange multiplier estimate to allow for high-accuracy solutions without driving p to infinity [6].
• Solution: Use a robust, second-order unconstrained optimization method (e.g., Newton's method) that can better handle ill-conditioned problems [15].

Numerical and Implementation Issues

FAQ: The solver for my unconstrained subproblem is failing to find a minimum. What should I check?

The success of SUMT hinges on reliably solving each unconstrained subproblem.

• Problem: The unconstrained solver fails to converge.
• Solution: Verify the smoothness of your penalized objective function. Non-differentiable penalty functions can cause problems for gradient-based solvers [16].
• Solution: Use the solution from the previous (lower p) unconstrained problem as the initial guess for the next one. This "warm-start" strategy often improves convergence [17].

FAQ: How can I handle a mix of equality and inequality constraints effectively?

The type of constraints influences the choice of the penalty function.

• Problem: Difficulty in satisfying equality constraints.
• Solution: It is often beneficial to eliminate equality constraints by solving for the dependent variables (xD) in terms of the independent ones (xI). This reduces the problem to one involving only inequality constraints, which are then handled by the penalty function [3]. The optimization is performed only over the independent variables xI.

Problem Formulation and Modeling

FAQ: How does the choice of penalty function impact the performance and solution quality?

Different penalty functions lead to different numerical behavior.

Table 1: Comparison of Common Penalty Functions

Penalty Function	Formulation (for ci(x) ≤ 0)	Key Characteristics
Quadratic	p * Σ (max(0, ci(x))^2 [6]	Smooth (differentiable), but may allow some infeasibility for finite p.
Deadzone-Linear [6]	Not specified in detail	Less sensitive to small violations, can be non-differentiable.
mBIC (Complex)	`3	T	log T + Σ log((t{k+1} - tk)/T)` [3]	Example of a complex, non-linear penalty; requires specialized optimization.

FAQ: When should I consider using SUMT over other constrained optimization algorithms?

SUMT is a versatile approach, but alternatives exist.

• Problem: Deciding whether SUMT is suitable.
• Solution: SUMT is attractive when you have efficient and robust unconstrained optimization solvers at your disposal. It is widely used in computational mechanics and engineering [6].
• Solution: For problems requiring high accuracy without extreme ill-conditioning, consider Barrier Methods (for strictly feasible interiors) or Augmented Lagrangian Methods (generally more robust) [6].

Experimental Protocols and Methodologies

Protocol 1: Basic SUMT with Quadratic Penalty for Drug Molecule Property Optimization

This protocol outlines the steps to optimize a molecular property (e.g., binding affinity) while constraining pharmacokinetic properties (e.g., solubility, toxicity) within a desired range, using a quadratic penalty method.

1. Problem Formulation:

• Objective Function: f(x) = -pKi (negative predicted binding affinity to be minimized).
• Inequality Constraints: c1(x) = logS_low - logS(x) ≤ 0, c2(x) = logS(x) - logS_high ≤ 0 (solubility within a range); c3(x) = Toxicity(x) - Toxicity_threshold ≤ 0.

2. Algorithm Setup:

• Penalty Function: Quadratic. P(x) = p * [ (max(0, c1(x)))^2 + (max(0, c2(x)))^2 + (max(0, c3(x)))^2 ].
• Penalty Parameter Sequence: Choose p0 = 1.0, update rule p_{k+1} = 5.0 * p_k.
• Convergence Tolerance: ε = 1e-6 for the norm of the gradient of the penalized objective, fp(x).
• Unconstrained Solver: Select a robust algorithm like L-BFGS-B or Newton-CG [16].

3. Execution:

• Step 1: Initialize p = p0 and an initial molecular design x0.
• Step 2: Minimize fp(x) = f(x) + P(x) using the chosen unconstrained solver.
• Step 3: If ||∇fp(x)|| < ε, check constraint violation. If all constraints are satisfied to a desired tolerance, terminate. Otherwise, proceed.
• Step 4: Update p = p_{k+1}.
• Step 5: Set the new initial point to the solution from Step 2. Return to Step 2.

Protocol 2: SUMT with Equality Constraint Elimination for Flow Sheet Optimization

This protocol is adapted from chemical engineering applications where process flowsheets must be optimized [3]. It demonstrates the elimination of equality constraints (simulating the convergence of the flowsheet) from the optimization problem.

1. Problem Formulation and Variable Partitioning:

• Variables: Identify and partition variables into independent (xI) and dependent (xD) sets. xI are the decision variables (e.g., reactor temperature, feed rate). xD are the variables determined by solving the process model equations (e.g., recycle stream compositions).
• Objective: min f(xI, xD) (e.g., maximize profit).
• Equality Constraints: c(xI, xD) = 0 (the process model equations).
• Inequality Constraints: g(xI, xD) ≤ 0 (safety, purity limits).

2. Penalty Function Setup:

• The optimization problem is re-written as: min_{xI} ψ(xI) = f(xI, xD(xI)) + p * ||g+(xI, xD(xI))|| [3], where xD(xI) is obtained by solving c(xI, xD) = 0 for any given xI.

3. Execution:

• Step 1: Make an initial guess for xI.
• Step 2: Inner Loop: Given xI, solve the equality constraints c(xI, xD) = 0 to obtain xD. This is equivalent to converging the flowsheet simulation [3].
• Step 3: Outer Loop: With xD now a function of xI, evaluate the penalized objective ψ(xI) and its gradient with respect to xI.
• Step 4: Use an unconstrained optimization method to update xI.
• Step 5: Repeat from Step 2 until convergence. The penalty parameter p can be increased sequentially for tighter satisfaction of the inequality constraints g(x).

Framework Visualization and Workflows

SUMT High-Level Workflow

SUMT Iterative Process

Troubleshooting Decision Tree

SUMT Problem Diagnosis

The Scientist's Toolkit: Research Reagent Solutions

Table 2: Essential Components for SUMT Implementation in Drug Discovery

Item / Reagent	Function / Role in the 'Experiment'
Unconstrained Optimization Solver	The core computational engine for minimizing the penalized objective function (e.g., L-BFGS, Conjugate Gradient, Newton's method) [16] [15].
Penalty Function (P(x))	The mathematical construct that incorporates constraints into the objective, quantifying violation (e.g., Quadratic, L1) [6].
Penalty Parameter Update Schedule	A predefined rule (e.g., multiplicative) for increasing the penalty parameter p to enforce constraint satisfaction [6].
Automatic Differentiation Tool	Software library to compute precise gradients and Hessians of the penalized objective, crucial for efficient solver performance [16].
Molecular Property Predictor	In-silico model (e.g., QSAR, AI-based) that predicts properties like toxicity or solubility for a candidate molecule, acting as the constraint function c(x) [18].
Molecular Generator / Sampler	A method to propose new candidate molecules (x); can be a simple sampler or a generative AI model for de novo design [18].

Exact Penalty Methods for Stress-Constrained Topology and Reliability Design

Frequently Asked Questions (FAQs)

Q1: What are the common causes of numerical instability when using exact penalty methods, and how can they be mitigated? Numerical instability in exact penalty methods often arises from the use of discontinuous operations like max and abs functions, which are inherent in traditional L1 exact penalty formulations. These discontinuities make the optimization procedure numerically unstable and are not suitable for gradient-based approaches [19]. Mitigation strategies include:

• Using a smooth, differentiable exact penalty function to avoid discontinuous operations [19].
• Implementing a smooth scheme for complementary conditions [19].
• Applying an adaptive adjusting scheme for the stress penalty factor to improve control over local stress levels and enhance convergence [20].

Q2: How do I select an appropriate penalty parameter/gain for stress-constrained topology optimization? Selecting a suitable penalty gain is crucial for the exact penalty method's performance. The process involves:

• A suitably selected gain is constructed using an active function inspired by topology optimization principles [19].
• For stress-constrained problems, an adaptive volume constraint and stress penalty method can be employed, where the penalty factor is adjusted to control the local stress level [20].
• The penalty term can be introduced to change the right-hand side (RHS) value of deterministic constraints without linearizing or transforming the limit-state function formulations [21].

Q3: My optimization converges to an infeasible design that violates stress constraints. What might be wrong? Convergence to an infeasible design typically indicates issues with constraint handling:

• The initial penalty parameter might be too small, providing insufficient constraint enforcement [19].
• The method may require a more robust active set detection. Consider using a differentiating active function to control the presence or absence of any constraint function [19].
• For stress-constrained problems, ensure proper integration of stress penalty with your optimization framework, potentially using the parametric level set method with compactly supported radial basis functions [20].

Q4: What is the relationship between the optimality conditions of the proposed penalty function and the traditional KKT conditions? The first-order necessary optimality conditions for the unconstrained optimization formulation using the exact penalty function maintain a direct relationship with the Karush-Kuhn-Tucker (KKT) conditions of the original constrained problem [19]. When the gradient of the proposed penalty function F(x) is set to zero, it yields conditions that relate to the traditional KKT conditions, ensuring theoretical consistency while avoiding the need for dual and slack variables [19].

Troubleshooting Guides

Problem: Poor Convergence in Reliability-Based Design Optimization (RBDO)

Symptoms: Slow convergence, oscillating design variables, or failure to reach feasible reliable design.

Solution Protocol:

• Implement Decoupled Approach: Transform the nested RBDO problem into sequential deterministic optimization and reliability analysis loops [21].
• Apply Penalty to Constraint RHS: Introduce penalty terms to change the right-hand side value of deterministic constraints rather than linearizing limit-state functions [21].
• Iterative Improvement: After determining mean values through initial deterministic optimization, perform reliability analysis and restructure the optimization problem with penalties to improve solutions iteratively [21].

Table: Key Parameters for RBDO Convergence

Parameter	Recommended Setting	Effect on Convergence
Penalty Type	RHS modification	Avoids approximation error from limit-state linearization [21]
Initial Multipliers	Prior knowledge exploitation	Improves starting point for iterative process [19]
Convergence Tolerance	Adaptive scheme	Balances accuracy and computational cost [21]

Problem: Computational Bottlenecks in Large-Scale Stress-Constrained Problems

Symptoms: Prohibitive computation time, memory issues, or inability to handle many constraints.

Solution Protocol:

• Eliminate Dual Variables: Use a differentiating exact penalty scheme that avoids unnecessary dual and slack variables for handling constraints [19].
• Apply Adaptive Schemes: Implement adaptive volume constraint and stress penalty methods to transform complex problems into simpler sub-problems [20].
• Utilize Efficient Solvers: For stress-penalty based compliance minimization, adopt the parametric level set method with compactly supported radial basis functions [20].

Table: Computational Efficiency Comparison of Methods

Method	Computational Features	Constraint Handling Approach
Traditional Lagrange Multiplier	High memory usage for dual variables [19]	Dual variables for each constraint [19]
Proposed Exact Penalty	Avoids dual/slack variables [19]	Differentiating active function [19]
Adaptive Volume-Stress Penalty	Transforms to simpler sub-problems [20]	Stress penalty with adaptive factor [20]

Problem: Handling Inactive/Active Constraints in Topology Optimization

Symptoms: Inability to properly identify which constraints are active, leading to suboptimal designs.

Solution Protocol:

• Implement Active Function: Design a differentiating active function inspired by topology optimization principles to indicate the existence of any constraint function [19].
• Develop Loss Functions: Create loss functions that measure constraint violation using a mapping relationship to measure constraint feasibility [19].
• Nested Formulation: For inequality constraints, use a nested form loss function by replacing the active function with the constraint function [19].

Experimental Protocols & Methodologies

Protocol 1: Smooth Exact Penalty Function Implementation

Purpose: To solve stress-constrained topology optimization without dual and slack variables [19].

Materials:

• Nonlinear constrained optimization problem with design variables x ∈ Rⁿ
• Objective function f(x) and constraint functions háµ¢(x) = 0, gâ±¼(x) ≤ 0
• Active function χ(x) based on topology optimization penalty principle

Procedure:

• Design Active Function: Create active function χ(x) = H[ψ(x)]·[ψ(x)]^κ where H is Heaviside function, ψ is constraint function [19].
• Construct Loss Functions: Develop loss functions for equality and inequality constraints using the active function framework [19].
• Formulate Penalty Function: Build the nested form penalty function incorporating constraint functions into loss functions [19].
• Solve Unconstrained Problem: Optimize the resulting unconstrained formulation using gradient-based methods [19].

Protocol 2: Adaptive Volume Constraint with Stress Penalty

Purpose: To obtain lightweight designs meeting stress constraints while optimizing compliance [20].

Materials:

• Structural domain with stress constraints
• Parametric level set method with compactly supported radial basis functions
• Adaptive penalty factor adjustment scheme

Procedure:

• Problem Transformation: Convert stress-constrained volume and compliance minimization into stress-penalty based compliance minimization and volume-decision sub-problems [20].
• Stress Penalty Application: Apply stress penalty to control local stress levels using parametric level set method [20].
• Adaptive Penalty Adjustment: Implement adaptive adjusting scheme for stress penalty factor to improve stress control [20].
• Volume Decision: Solve volume-decision problem using combination scheme of interval search and local search [20].

Research Reagent Solutions

Table: Essential Computational Tools for Exact Penalty Methods

Tool/Component	Function/Purpose	Implementation Notes
Differentiating Active Function	Indicates existence of constraint functions [19]	Based on topology optimization penalty principle
Nested Loss Functions	Measures constraint violation [19]	Replaces constraint functions in penalty formulation
Adaptive Penalty Factor	Controls local stress levels [20]	Requires careful adjustment scheme
Parametric Level Set Method	Solves stress-penalty compliance minimization [20]	Uses compactly supported radial basis functions
Heaviside Function Approximation	Enables smooth transitions in active functions [19]	Critical for numerical stability

Workflow Visualization

Exact Penalty Method Workflow

Constraint Handling Transformation

Quadratic Unconstrained Binary Optimization (QUBO) in Peptide-Protein Docking

Frequently Asked Questions (FAQs)

What is the primary advantage of using a QUBO formulation for peptide-protein docking? The primary advantage is the ability to leverage quantum-amenable optimization solvers, such as quantum annealers or variational algorithms, to find optimal docking conformations. The QUBO formulation translates the complex biological problem of finding a peptide's 3D structure on a target protein into a minimization problem of a quadratic function of binary variables, which is a standard input for these solvers [22] [23].

How are physical constraints, like preventing atomic clashes, incorporated into the QUBO model? Physical constraints are incorporated by adding penalty terms to the QUBO Hamiltonian. For example, a steric clash constraint is enforced by adding a high-energy penalty to the objective function whenever two peptide particles or a peptide particle and a blocked protein site are placed on the same lattice vertex. The use of appropriate penalty weights is critical to ensure that these constraints are satisfied in the optimal solution [22] [24].

My QUBO model fails to find feasible solutions that satisfy all cyclization constraints. What could be wrong? This is often a problem of penalty function tuning. The Hamiltonian term for cyclization (H_cycle) must be assigned a sufficiently high penalty weight to make any solution violating the cyclization bond energetically unfavorable compared to feasible solutions. If the weight is too low, the solver may prioritize lower interaction energy over satisfying the constraint. A systematic hyperparameter search, for instance using Bayesian optimization, is recommended to find the correct balance [23] [25].

Why does my QUBO model scale poorly with increasing peptide residues? The QUBO formulation for lattice-based docking is an NP-complete problem. The number of binary variables required grows rapidly with the number of peptide residues and the size of the protein's active site, quickly exceeding the capacity of current classical and quantum hardware. Research indicates that QUBO models using simulated annealing can find feasible conformations for peptides with up to 6 residues but struggle with larger instances [22] [23] [24].

What is a viable classical alternative if my QUBO model does not scale? Constraint Programming (CP) is a powerful classical alternative. Unlike QUBO, which combines objectives and constraints into a single penalty function, CP uses a declarative approach to explicitly define variables, their domains, and constraints. This allows CP solvers to efficiently prune the search space. Studies have shown that CP models can find optimal solutions for problems with up to 11-13 peptide residues, where QUBO models fail [22] [23] [25].

Troubleshooting Guides

Problem: Solver Returns High-Energy or Non-Native Conformations

This occurs when the predicted peptide structure has a high (unfavorable) Miyazawa-Jernigan (MJ) interaction energy or a high Root Mean Square Deviation (RMSD) from the known native structure.

Potential Cause	Diagnostic Steps	Solution
Incorrect penalty weight in H_protein for steric clashes.	Check if any peptide residues are placed on lattice vertices within the blocking radius (e.g., 3.8Ã…) of the protein.	Increase the penalty weight for the steric hindrance term in H_protein to completely forbid such placements [23] [24].
Poorly tuned QUBO hyperparameters.	Perform a sensitivity analysis on the weights of the different Hamiltonian terms (H_comb, H_back, H_cycle, H_protein).	Use automated hyperparameter optimization (e.g., Bayesian optimization via Amazon SageMaker) to find parameter sets that yield low-energy, feasible solutions [23].
Discretization error from the lattice.	Compare the continuous atomic coordinates from the PDB with the discrete lattice vertices. A fundamental error is introduced.	Consider using a finer-grained lattice or a post-processing step with continuous energy minimization to refine the lattice-based solution [26].

Problem: Model Fails to Scale Beyond Small Peptides

This refers to the inability to find a solution for peptides with more than approximately 6 residues within a reasonable time or memory footprint.

Potential Cause	Diagnostic Steps	Solution
Combinatorial explosion of the problem space.	Monitor the rapid growth in the number of binary variables as peptide length increases.	For larger peptides, switch to a Constraint Programming (CP) approach, which has been demonstrated to handle larger instances effectively [22] [25].
Inefficient encoding strategy.	Analyze the number of variables used by your encoding (e.g., spatial vs. turn encoding).	Adopt a "resource-efficient" turn encoding, which has been shown to require fewer variables than spatial encodings for representing peptide chains [22] [24].
Limitations of the classical solver.	If using simulated annealing, observe the solution quality plateauing with increased runtime.	For QUBO models, experiment with more advanced hybrid solvers or, if available, quantum annealing hardware to explore if they offer better scaling properties [27].

Experimental Protocols & Data

Standardized Docking Pipeline

The following workflow, derived from published research, ensures a consistent and reproducible process for preparing and solving docking problems [23].

Performance Benchmarking Data

The table below summarizes the performance of QUBO (solved with simulated annealing) versus Constraint Programming (CP) on real peptide-protein complexes from the Protein Data Bank (PDB). This data provides a benchmark for expected performance [23].

PDB ID	Peptide Residues	Protein Residues	Method	MJ Potential	RMSD (Ã…)	Feasible Found?
3WNE	6	26	QUBO	-28.53	8.88	Yes
			CP	-42.64	8.48	Yes
5LSO	6	34	QUBO	-17.93	7.68	Yes
			CP	-23.26	10.29	Yes
3AV9	8	28	QUBO	--	--	No
			CP	-40.44	8.98	Yes
2F58	11	49	QUBO	--	--	No
			CP	Solved	Solved	Yes

The Scientist's Toolkit: Key Research Reagents

This table details the essential components and their functions for constructing and solving QUBO models for peptide-protein docking.

Item	Function in the Experiment	Technical Specification
Tetrahedral Lattice	Provides a discrete 3D space to model peptide conformation, reducing the problem from continuous to combinatorial search [22] [24].	A set of vertices (\mathcal{T}) in 3D space with tetrahedral coordination.
Coarse-Grained (CG) Representation	Simplifies the molecular system, reducing computational complexity. Each amino acid is represented by 1-2 particles (main chain and side chain) [23] [24].	Two-particle model for standard residues; one-particle for Glycine.
Miyazawa-Jernigan (MJ) Potential	A scoring function that estimates the interaction energy between amino acid residues, used as the objective to minimize [22] [26].	Lookup table of fixed interaction potentials for unique pairs of amino acid types.
QUBO Hamiltonian (H)	The core mathematical model that integrates all problem objectives and constraints into a single quadratic function of binary variables [22] [24].	(H = H\textrm{comb} + H\textrm{back} + H\textrm{cycle} + H\textrm{protein})
Steric Clash Radius	Defines the minimal allowed distance between atoms, preventing physically impossible overlapping conformations [23].	Typically set to 3.8Ã… for determining which lattice vertices are blocked by the protein.
Protein Active Site	A focused region of the target protein where docking is likely to occur, drastically reducing the search space and computational cost [23] [24].	Residues within a specified distance (e.g., 5Ã…) from the peptide in the native complex.

QUBO Framework Diagram

The following diagram illustrates the logical structure of the full QUBO Hamiltonian, showing how different constraints and objectives are combined using penalty functions [22] [23] [24].

Constrained Multi-Objective Molecular Optimization (CMOMO) for Drug-like Candidates

Constrained Multi-Objective Molecular Optimization (CMOMO) represents an advanced artificial intelligence framework specifically designed to address the complex challenges of molecular discovery in drug development. This approach simultaneously optimizes multiple molecular properties while adhering to stringent drug-like constraints, which is a critical requirement in practical pharmaceutical applications [28]. Traditional molecular optimization methods often neglect essential constraints, limiting their ability to produce viable drug candidates. CMOMO addresses this gap by implementing a sophisticated penalty-based constraint handling mechanism within a multi-objective optimization framework, enabling researchers to identify molecules that balance optimal property profiles with strict adherence to drug-like criteria [29].

The foundation of CMOMO rests on formulating molecular optimization as a constrained multi-objective problem, where each property to be enhanced is treated as an optimization objective, and stringent drug-like criteria are implemented as constraints. This formulation differs significantly from both single-objective optimization and unconstrained multi-objective optimization, as it must navigate the challenges of narrow, disconnected, and irregular feasible molecular spaces caused by constraint imposition [28]. The framework employs a dynamic cooperative optimization strategy that evolves molecules in continuous latent space while evaluating properties in discrete chemical space, creating an effective mechanism for discovering high-quality candidate molecules.

Key Concepts and Definitions

Constrained Multi-Objective Optimization in Molecular Context

In CMOMO, constrained multi-property molecular optimization problems are mathematically expressed as:

min F(x) = (f₁(x), f₂(x), …, fₘ(x)) subject to gᵢ(x) ≤ 0, ∀i ∈ {1, …, p} hⱼ(x) = 0, ∀j ∈ {1, …, q} x ∈ 𝒮

Where x represents a molecule within the molecular search space 𝒮, F(x) is the objective vector comprising m optimization properties, and gᵢ(x) and hⱼ(x) are inequality and equality constraints, respectively [28].

Constraint Violation Measurement

The Constraint Violation (CV) function quantitatively measures the degree to which a molecule violates constraints:

$$CV(x) = \sum{i=1}^{p} \max(0, gi(x)) + \sum{j=1}^{q} |hj(x)|$$

A molecule is considered feasible when CV(x) = 0, and infeasible otherwise [28]. This metric enables the algorithm to prioritize molecules that better satisfy constraints during the optimization process.

Multi-Objective Optimization Fundamentals

Multi-objective optimization differs fundamentally from single-objective approaches by seeking a set of optimal solutions representing trade-offs among competing objectives, rather than a single optimal solution. In molecular design, this approach reveals the complex relationships between various molecular properties, providing researchers with multiple candidate options along the Pareto front [30] [31]. This is particularly valuable in drug discovery, where researchers must balance conflicting requirements such as potency, solubility, and metabolic stability.

Experimental Protocols and Methodologies

CMOMO Workflow Implementation

The CMOMO framework implements a structured two-stage optimization process:

• Population Initialization:

  • Given a lead molecule represented as a SMILES string, CMOMO first constructs a Bank library containing high-property molecules similar to the lead molecule from public databases
  • A pre-trained encoder embeds the lead molecule and Bank library molecules into a continuous latent space
  • Linear crossover between the latent vector of the lead molecule and those in the Bank library generates a high-quality initial molecular population [28] [29]

• Dynamic Cooperative Optimization:

  • Unconstrained Scenario: CMOMO employs a Vector Fragmentation-based Evolutionary Reproduction (VFER) strategy on the implicit molecular population to efficiently generate offspring in continuous latent space
  • Molecules are decoded from latent space to discrete chemical space using a pre-trained decoder for property evaluation
  • Environmental selection based on NSGA-II principles selects molecules with better property values for the next generation
  • Constrained Scenario: After reaching iteration limits in the unconstrained phase, CMOMO switches to constrained optimization, using a ranking aggregation strategy to evaluate and select molecules by balancing property optimization and constraint satisfaction [29]

Benchmarking and Validation Protocols

To validate CMOMO performance, researchers should implement the following experimental protocol:

• Dataset Preparation:

  • Select benchmark molecular optimization tasks with clearly defined objectives and constraints
  • Curate lead molecules representing starting points for optimization
  • Define property evaluation metrics and constraint criteria

• Algorithm Configuration:

  • Set population size and iteration parameters for each optimization stage
  • Configure VFER parameters for latent space exploration
  • Define constraint violation thresholds and penalty parameters

• Performance Assessment:

  • Compare against state-of-the-art baselines (QMO, Molfinder, MOMO, MSO, GB-GA-P)
  • Evaluate success rate: percentage of successfully optimized molecules satisfying all constraints
  • Assess property improvement metrics across multiple objectives
  • Analyze diversity and novelty of generated molecular candidates [28]

Research Reagent Solutions

Table 1: Essential Computational Tools and Resources for CMOMO Implementation

Resource Category	Specific Tool/Resource	Function in CMOMO Workflow
Molecular Representation	SMILES Strings	Represent molecular structures in standardized textual format [28] [29]
Chemical Informatics	RDKit	Handle molecular validity verification and basic chemical property calculation [28]
Latent Space Modeling	Pre-trained Encoder-Decoder	Transform molecules between discrete chemical space and continuous latent representations [28] [29]
Optimization Framework	NSGA-II Implementation	Perform environmental selection based on non-dominated sorting and crowding distance [29]
Constraint Handling	Custom CV Calculator	Quantify constraint violation degrees for molecular candidates [28]
Property Prediction	QSAR Models (e.g., CatBoost)	Predict biological activity and ADMET properties from molecular structures [31]

Troubleshooting Guides and FAQs

Common Implementation Challenges and Solutions

Problem 1: Poor Optimization Performance

Q: Why does CMOMO fail to identify molecules that simultaneously satisfy constraints and show property improvements?

A: This issue typically stems from improper balance between the unconstrained and constrained optimization phases.

Solution:

• Adjust the transition criteria between optimization stages
• Implement adaptive penalty parameters that evolve based on population feasibility rates
• Verify the diversity preservation mechanisms in environmental selection
• Ensure the latent space fragmentation in VFER maintains sufficient exploration capability [28] [29]

Problem 2: Invalid Molecular Structures

Q: Why does the decoder generate invalid molecular structures from latent representations?

A: This occurs due to discontinuities between the continuous latent space and valid chemical space.

Solution:

• Fine-tune the pre-trained encoder-decoder on relevant chemical domains
• Implement validity checks before property evaluation
• Apply structural correction algorithms to repair invalid structures
• Adjust VFER parameters to remain within regions of latent space that decode to valid molecules [28]

Problem 3: Infeasible Solution Populations

Q: Why does CMOMO struggle to find molecules satisfying all constraints, even when feasible solutions should exist?

A: This suggests issues with constraint handling or exploration in highly constrained spaces.

Solution:

• Implement dynamic constraint relaxation in early generations
• Employ feasibility-based selection when few feasible solutions exist
• Modify the CV aggregation function to better guide search toward feasible regions
• Combine penalty-based approaches with repair mechanisms for specific constraint types [28] [32]

Problem 4: Computational Resource Limitations

Q: How can I manage CMOMO's computational demands for large-scale molecular optimization?

A: Several strategies can improve computational efficiency.

Solution:

• Implement batch processing for property evaluation
• Use surrogate models for expensive property predictions
• Apply filtering mechanisms to avoid evaluating obviously poor candidates
• Optimize population sizes based on problem complexity [29]

Performance Optimization FAQs

Q: How should I set penalty parameters for different constraint types? A: Penalty parameters should reflect constraint importance and violation scales. Implement adaptive penalties that increase as optimization progresses, forcing final solutions to satisfy all constraints [32].

Q: What criteria determine when to switch from unconstrained to constrained optimization? A: Transition based on performance plateau detection in the unconstrained phase, measured by improvement in hypervolume or generational distance metrics over successive iterations [28] [29].

Q: How can I handle conflicting constraints in molecular optimization? A: Analyze constraint relationships before optimization. For strongly conflicting constraints, consider hierarchical prioritization or constraint relaxation strategies [28].

Workflow Visualization

CMOMO Two-Stage Optimization Workflow

Performance Benchmarking

Table 2: CMOMO Performance Comparison on Benchmark Tasks

Evaluation Metric	CMOMO	QMO	Molfinder	MOMO	MSO	GB-GA-P
Success Rate (%)	85.7	42.3	38.5	31.2	52.6	46.8
Property Improvement (Avg %)	62.4	35.2	32.8	41.5	28.7	25.3
Constraint Satisfaction (%)	96.2	74.5	69.8	65.3	82.4	88.7
Diversity Index	0.82	0.65	0.58	0.79	0.61	0.54
Computational Time (Relative)	1.00	0.85	0.92	0.78	1.12	1.24

Table 3: CMOMO Application Results on Practical Drug Discovery Tasks

Optimization Task	Baseline Molecule	CMOMO Optimized Molecule	Property Improvement (%)	Constraint Satisfaction (%)
4LDE Protein Ligand	Initial lead compound	CMOMO candidate #12	Bioactivity: 45.2%Drug-likeness: 28.7%Synthetic Accessibility: 15.3%	100% (Structural constraints)
GSK3β Inhibitor	Known inhibitor scaffold	CMOMO candidate #47	Bioactivity: 67.8%Drug-likeness: 32.5%Toxicity: 41.2%	100% (Structural alerts)

Advanced Methodologies

Penalty Function Implementation in CMOMO

CMOMO implements a sophisticated penalty approach that dynamically adjusts based on search progress and population characteristics. The penalty-integrated fitness function can be represented as:

Φ(x) = F(x) × (1 + CV(x) × λ(t))

Where λ(t) is a dynamically adjusted penalty coefficient that increases with generation number t, progressively emphasizing constraint satisfaction as optimization progresses [32]. This approach differs from static penalty methods by allowing greater exploration in early stages while enforcing constraint satisfaction in final solutions.

Vector Fragmentation-based Evolutionary Reproduction (VFER)

The VFER strategy represents a key innovation in CMOMO, enhancing search efficiency in continuous latent space:

• Latent Vector Segmentation: Divide latent representations into meaningful fragments corresponding to molecular substructures
• Fragment-based Crossover: Implement specialized recombination operations that preserve chemically meaningful building blocks
• Directed Mutation: Apply mutation operators biased toward regions of latent space decoding to molecules with improved properties
• Elitism Preservation: Maintain best-performing solutions across generations to prevent quality regression [28] [29]

This approach significantly enhances the efficiency of molecular exploration compared to standard evolutionary operations.

CMOMO represents a significant advancement in constrained multi-objective molecular optimization by effectively balancing property improvement with strict constraint satisfaction. The framework's two-stage optimization approach, combined with sophisticated constraint handling through penalty functions and specialized evolutionary operators, enables the discovery of high-quality drug candidates that simultaneously excel across multiple properties while adhering to critical drug-like criteria. As molecular optimization continues to play an increasingly important role in accelerating drug discovery, CMOMO provides researchers with a powerful methodology for navigating complex design spaces with multiple competing objectives and constraints.

Kernel-Based Models for Predicting Drug-Target Interactions

Frequently Asked Questions (FAQs)

FAQ 1: What is the core principle behind kernel-based models for DTI prediction?

Kernel-based models operate on the fundamental idea that similar drugs tend to interact with similar target proteins. These methods use kernel functions to compute similarity matrices between drugs (based on structures, side effects, etc.) and between targets (based on sequences, functions, etc.). A pairwise kernel, often constructed via the Kronecker product of the drug and target kernels, then defines the similarity between drug-target pairs, which is used to predict new interactions. [33]

FAQ 2: My model performance is poor. Could inadequate feature integration be the cause?

Yes, limited performance is often due to relying on a single, potentially weak, data source for drug or target similarity. It is recommended to use a Multiple Kernel Learning (MKL) approach. MKL frameworks, like KronRLS-MKL, allow the integration of multiple heterogeneous information sources (e.g., various drug kernels and target kernels) and automatically learn the optimal weights for each kernel, which often significantly improves predictive performance. [33]

FAQ 3: How do penalty functions integrate with kernel-based DTI models?

Penalty functions are a class of algorithms for solving constrained optimization problems by transforming them into a series of unconstrained problems. In the context of kernel-based DTI prediction, penalty methods can enforce constraints during model training. For instance, they can be used to ensure that predicted binding affinities adhere to known biochemical boundaries or to incorporate prior knowledge about specific drug-target pairs directly into the optimization objective of the model. [6]

FAQ 4: What are the main computational challenges when working with large-scale DTI datasets?

A primary challenge is the memory requirement. For ( nd ) drugs and ( nt ) targets, the full pairwise kernel matrix has ( nd * nt ) rows and columns, making its explicit computation and storage infeasible for large datasets. Algorithms like KronRLS address this by leveraging algebraic properties of the Kronecker product, such as the "vec trick," to avoid constructing the massive matrix directly, enabling predictions on the entire drug-target interaction space. [33]

FAQ 5: Are there quantum computing alternatives to classical kernel methods for DTI?

Yes, recent research proposes quantum-enhanced frameworks. For example, the QKDTI model uses a Quantum Support Vector Regression (QSVR) with quantum feature mapping. This approach encodes classical molecular and protein features into quantum states within a Hilbert space, potentially capturing complex, non-linear interactions through quantum entanglement and interference, which may lead to improved predictive accuracy and generalization. [34]

Troubleshooting Guides

Problem 1: Model fails to generalize to novel drugs or targets ("cold start problem").

• Symptoms: High accuracy for known drug-target pairs but poor performance when predicting interactions for new drugs (with no known interactions) or new targets.
• Possible Causes:
  • The model is overly reliant on interaction data alone and lacks robust similarity measures for cold-start entities.
  • The chosen kernel for drugs or targets does not adequately capture the features that determine interaction for unseen entities.
• Solutions:
  • Enrich Similarity Kernels: For new drugs, integrate multiple chemical descriptors (e.g., fingerprints, functional groups) and clinical information (e.g., side effects). For new targets, use diverse sequence, structural, and genomic data. [35] [33]
  • Utilize MKL: Implement a multiple kernel learning algorithm that can weight different data sources automatically, emphasizing the most predictive kernels for the task. [33]
  • Leverage Bipartite Network Methods: Use methods that explicitly model the DTI problem as a link prediction task on a bipartite network, which can help propagate information across the network. [33]

Problem 2: Training the model is computationally infeasible on a large dataset.

• Symptoms: The program runs out of memory or takes an impractically long time to train.
• Possible Causes:
  • Attempting to build the full pairwise kernel matrix for all possible drug-target pairs, which has a size of ( (nd * nt) \times (nd * nt) ).
• Solutions:
  • Use Efficient Algorithms: Employ specialized algorithms like KronRLS or its MKL extension (KronRLS-MKL). These methods use the Kronecker product identity and eigenvalue decomposition to avoid explicitly constructing the massive kernel matrix, drastically reducing memory and computational requirements. [33]
  • Apply the Nyström Approximation: As demonstrated in the QKDTI model, integrate the Nyström approximation into your kernel method. This technique provides an efficient low-rank approximation of the kernel matrix, significantly reducing computational overhead. [34]

Problem 3: The model's predictions lack interpretability.

• Symptoms: The model provides a binding score but gives no insight into why a particular drug-target pair was predicted to interact.
• Possible Causes:
  • Kernel methods, like other "black-box" models, can be difficult to interpret as they operate in high-dimensional feature spaces.
• Solutions:
  • Analyze Kernel Weights: If using an MKL approach, examine the weights assigned to each drug and target kernel. Kernels with higher weights are more relevant for the prediction task and can reveal which data sources (e.g., side effects, target sequences) are most informative. [35] [33]
  • Implement a Hybrid Model: Combine kernel methods with more interpretable models or use post-hoc interpretation tools to analyze the model's decisions on specific predictions.

The table below summarizes the performance of various DTI prediction models on benchmark datasets as reported in the literature.

Table 1: Performance Comparison of DTI Prediction Models on Benchmark Datasets [34]

Model / Framework	Type	Dataset	Accuracy (%)	Key Features
QKDTI	Quantum Kernel	DAVIS	94.21	Quantum feature mapping, QSVR, Nyström approximation [34]
		KIBA	99.99
		BindingDB	89.26
KronRLS-MKL	Classical MKL	Multiple Datasets	Higher or comparable to 18 competing methods	Multiple kernel integration, automatic kernel weighting, efficient Kronecker product computation [33]
MK-TCMF	Classical MKL	Four Test Datasets	Better performance than other computational methods	Triple collaborative matrix factorization, integrates chemical, biological, and clinical information [35]

Table 2: Common Kernel Types for Drug and Target Similarity [33]

Entity	Kernel Type	Description	Information Source
Drug	Structural Similarity	Based on 2D or 3D molecular structure comparison	Chemical structure (e.g., SMILES)
	Target Profile	Based on shared target proteins	Previous bioactivity data
	Side-effect Similarity	Based on shared side effects	Clinical data
	Pharmacophore	Based on common chemical features	Molecular fingerprints
Target	Sequence Similarity	Based on amino acid sequence alignment	Protein sequence data
	Functional Similarity	Based on Gene Ontology (GO) terms	Genomic & functional data
	PPI Network	Based on proximity in a Protein-Protein Interaction network	Network data
	Structural Similarity	Based on 3D protein structure	PDB files

Experimental Protocols

Protocol 1: Implementing a Multiple Kernel Learning (MKL) Pipeline for DTI Prediction

This protocol outlines the steps for building a KronRLS-MKL model. [33]

• Data Collection & Preprocessing:

  • Obtain a DTI dataset (e.g., from Davis, KIBA, or BindingDB) containing known drug-target pairs with binding affinities or binary interaction labels. [34]
  • Compile diverse drug information (chemical structure, side effects, etc.) and target information (sequence, GO terms, etc.).

• Kernel Matrix Calculation:

  • For each type of drug information, compute a drug kernel matrix ( K_D^{(i)} ) where each entry represents the similarity between two drugs.
  • For each type of target information, compute a target kernel matrix ( K_T^{(j)} ).
  • Normalize all kernel matrices.

• Model Training with KronRLS-MKL:

  • Objective: The extended KronRLS minimizes a loss function that incorporates multiple kernels. The minimization function for the dual variables with multiple kernels is derived from the following base KronRLS formulation: [33] J(f) = (1/(2n)) * Σ(y_i - f(x_i))² + (λ/2) * ||f||_K²
  • The combined kernel is a weighted sum of the individual Kronecker product kernels: K = Σ θ_d(i) * K_D(i) ⊗ Σ θ_t(j) * K_T(j).
  • The algorithm optimizes the weights ( \thetad ) and ( \thetat ) for the drug and target kernels simultaneously with the model parameters.

• Prediction & Evaluation:

  • Use the trained model to predict interactions for unknown drug-target pairs.
  • Evaluate performance using standard metrics like Area Under the Curve (AUC), Accuracy, and Precision-Recall on held-out test data.

Protocol 2: Quantum Kernel Feature Mapping for Molecular Data

This protocol describes the quantum feature mapping process used in the QKDTI model. [34]

• Classical Feature Encoding:

  • Represent drugs and targets using classical molecular descriptors (e.g., ECFP fingerprints for drugs, amino acid physicochemical properties for targets).

• Quantum Feature Mapping:

  • Encode the classical feature vectors into a quantum state using a parameterized quantum circuit.
  • The QKDTI framework uses RY and RZ rotation gates to create a quantum feature map, which transforms the classical data into a high-dimensional quantum Hilbert space.

• Quantum Kernel Estimation:

  • The quantum kernel between two data points ( xi ) and ( xj ) is defined as the inner product of their quantum feature maps: ( K(xi, xj) = |⟨φ(xi)|φ(xj)⟩|² ).
  • This kernel is computed on a quantum computer (or simulator).

• Model Training with QSVR:

  • The computed quantum kernel is used within a classical Support Vector Regression (SVR) algorithm to learn the mapping between drug-target pairs and their binding affinity, completing the hybrid quantum-classical pipeline.

Workflow and Relationship Visualizations

The Scientist's Toolkit

Table 3: Key Research Reagent Solutions for Kernel-Based DTI Prediction

Item / Resource	Function in DTI Research
ChEMBL Database [36]	A manually curated database of bioactive molecules with drug-like properties. It provides chemical, bioactivity, and genomic data essential for building and testing DTI models.
Davis / KIBA / BindingDB Datasets [34]	Benchmark datasets containing verified drug-target interactions with binding affinity data (e.g., Kd, Ki, IC50). Used for training models and standardized performance comparison.
Multiple Kernel Learning (MKL) Framework [33]	A computational method that integrates multiple similarity measures (kernels) for drugs and targets, automatically learning their importance to improve prediction accuracy.
Kronecker Regularized Least Squares (KronRLS) [33]	An efficient algorithm for large-scale DTI prediction. It avoids the computational burden of building a full pairwise kernel matrix by using Kronecker product algebra.
Quantum Kernel Feature Mapping [34]	A technique using parameterized quantum circuits (e.g., with RY/RZ gates) to map classical molecular data into a high-dimensional quantum feature space, potentially capturing complex patterns.
Nyström Approximation [34]	A mathematical technique used to provide a low-rank approximation of a kernel matrix. It reduces the computational and memory overhead of kernel methods, making them more feasible.
Penalty Function Method [6]	An optimization technique for handling constraints by adding a penalty term to the objective function. In DTI, it can enforce biochemical constraints on predicted binding affinities.

Overcoming Practical Challenges: Numerical Stability and Parameter Selection

Core Concepts: Ill-Conditioning in Penalty Methods

What is the fundamental relationship between large penalty parameters and ill-conditioning?

In penalty methods for constrained optimization, a large penalty parameter p is necessary to enforce constraint satisfaction. However, as p grows, the unconstrained penalized objective function becomes ill-conditioned. This occurs because the Hessian matrix of the penalized objective function develops a high condition number, meaning small changes in input can cause large variations in output, leading to numerical instability, slow convergence, and increased sensitivity to rounding errors [6] [37].

Mathematical Formulation: For a constrained problem:

The penalty method transforms this into:

where g measures constraint violation (e.g., g(z) = max(0,z)^2). As p → ∞, the condition number of the Hessian ∇²f_p(x) grows, making the problem increasingly difficult to solve numerically [6].

Troubleshooting FAQs

Why does my optimization stagnate or diverge when I increase the penalty parameter?

This is a classic symptom of ill-conditioning induced by large penalty parameters. As the penalty parameter increases, the objective function's curvature becomes increasingly uneven, causing gradient-based methods to take excessively small steps or oscillate. The condition number of the Hessian matrix grows with the penalty parameter, amplifying numerical errors in computations [6] [37].

Diagnostic Steps:

• Monitor the condition number of your Hessian (or its approximation)
• Check if the norm of the solution vector x becomes unusually large
• Verify if constraint violations decrease extremely slowly despite large p
• Examine step sizes in iterative methods - ill-conditioning causes tiny steps

How can I identify ill-conditioning in my penalty method implementation?

Ill-conditioning manifests through several observable behaviors in your optimization process [37] [38]:

• Slow Convergence: Optimization progress stalls despite significant computational effort
• Numerical Instability: Small changes in parameters or data cause large changes in solutions
• Catastrophic Cancellation: Significant loss of precision in floating-point calculations
• Sensitivity to Initial Conditions: Different starting points yield dramatically different results
• High Residual Norms Relative to Solution Norm: The relative residual ‖b - A*x‖/(‖A‖*‖x‖) might be misleadingly small while the solution is inaccurate [38]

Quick Diagnostic Table:

Symptom	Measurement Method	Threshold for Concern
Slow convergence	Iteration count vs progress	Minimal improvement over 50+ iterations
High condition number	Compute κ = σmax/σmin	κ > 10^6 for double precision
Solution sensitivity	Perturb inputs slightly	> 10% change in solution from 0.1% input change
Large solution norm	‖x‖	Growing rapidly with penalty increases

Mitigation Strategies

What techniques can alleviate ill-conditioning from large penalty parameters?

Strategy	Mechanism	Best For	Limitations
Preconditioning	Transforms problem to reduce condition number	Linear systems, conjugate gradient methods	Requires finding effective preconditioner
Regularization	Adds small stabilizing terms to the problem	Ill-posed inverse problems	Slightly biases solution
Augmented Lagrangian	Combines penalty with Lagrange multipliers	Avoiding p → ∞ while maintaining accuracy	More complex implementation
Variable Scaling	Normalizes variables to similar magnitudes	Poorly scaled problems	May not address fundamental ill-conditioning
Mixed-Precision Arithmetic	Uses higher precision for critical operations	Minimizing roundoff error accumulation	Increased computational cost
Problem Reformulation	Changes basis or mathematical structure	Artificially induced ill-conditioning	Problem-specific approach

Implementation Details for Key Strategies:

Augmented Lagrangian Method: This approach combines the penalty method with Lagrange multipliers, allowing for satisfactory constraint enforcement without driving the penalty parameter to infinity. The method alternates between optimizing the augmented Lagrangian and updating the multiplier estimates [6].

Preconditioning Techniques:

• Diagonal Scaling: Use P = diag(A) for diagonal-dominant systems
• Incomplete LU Factorization: Effective for sparse matrices
• Jacobian Preconditioning: Suitable for diagonally dominant systems [37]

Tikhonov Regularization: Adds a small term to the objective: f_p(x) + δ‖x‖² where δ is a small regularization parameter (typically 10^-6 to 10^-8). This stabilizes the Hessian without significantly altering the solution [37].

Experimental Protocols

Protocol 1: Condition Number Monitoring During Penalty Method

Objective: Track how condition number evolves with increasing penalty parameters.

Materials:

• Optimization problem with constraints
• Penalty method implementation
• Matrix condition number estimator (power method or SVD-based)

Procedure:

• Initialize penalty parameter p = p_0
• For k = 1 to K_max: a. Solve unconstrained problem: min f(x) + p_k * Σ g(c_i(x)) b. Compute/estimate condition number of Hessian at solution c. Record solution norm, constraint violation, and condition number d. Increase penalty parameter: p_{k+1} = γ * p_k (typically γ = 10)
• Plot condition number vs penalty parameter and vs solution quality

Expected Outcome: Exponential growth of condition number with linear increase in penalty parameter.

Protocol 2: Comparative Analysis of Ill-Conditioning Mitigation Methods

Objective: Evaluate effectiveness of different strategies for managing ill-conditioning.

Materials:

• Test problems with known ill-conditioning issues
• Implementation of multiple mitigation strategies
• Performance metrics: iteration count, solution accuracy, computation time

Procedure:

• Select benchmark optimization problems with constraints
• Apply standard penalty method with large p as baseline
• Implement each mitigation strategy:
  • Augmented Lagrangian method
  • Preconditioned penalty method
  • Regularized penalty method
• Measure performance metrics for each approach
• Compare results across normalization factors (solution quality vs computational cost)

Validation Metrics:

• Final objective value relative to known optimum
• Constraint satisfaction level
• Iteration count to convergence
• Computational time
• Numerical stability across multiple runs

Research Reagent Solutions

Research Reagent	Function	Application Context
LAPACK	Dense linear algebra with condition estimation	Condition number calculation for Hessians
SUNDIALS	Nonlinear solver suite with preconditioning	Large-scale optimization problems
PETSc	Portable toolkit for scientific computation	Preconditioning for distributed systems
Eigen	C++ template library for linear algebra	Embedded condition number estimation
ARPACK	Large-scale eigenvalue problem solver	Spectral analysis of Hessian matrices
Matrix Market	Repository of test matrices	Ill-conditioned benchmark problems

Workflow Diagrams

Diagram 1: Penalty Optimization with Ill-Conditioning Mitigation

Diagram 2: Ill-Conditioning Mitigation Decision Pathway

Troubleshooting Guides

Guide 1: My optimization fails to converge to a feasible solution

• Problem: The solver runs but returns a solution that significantly violates the constraints.
• Diagnosis: This is often a sign of an incorrectly chosen penalty parameter.
  • Parameter Too Small: If the penalty parameter (ρ, μ, or ν) is too small, the optimizer may find it "cheaper" to accept constraint violations than to satisfy them, leading to infeasible solutions [3].
  • Parameter Too Large: Conversely, a very large penalty parameter can make the unconstrained penalized problem ill-conditioned. This leads to a landscape with sharp curvature, causing slow convergence or failure of the unconstrained minimization algorithm [6] [3].
• Solution:
  • Use an Adaptive Strategy: Implement an iterative strategy where you start with a moderate penalty parameter, solve the unconstrained problem, and then increase the parameter for the next run if the solution is infeasible. Repeat until convergence to a feasible point is achieved [39] [6].
  • Check the Formulation: Ensure your penalty function correctly measures constraint violation (e.g., using squared violation for equality constraints) [6].

Guide 2: How do I tune multiple penalty parameters simultaneously?

• Problem: Methods like the Elastic Net or complex penalty functions involve more than one penalty parameter. Tuning them is non-trivial [40] [41].
• Diagnosis: There is often no theoretical backing for a fixed ratio between multiple parameters. Simultaneous tuning can be computationally expensive and the parameters can be hard to identify [40].
• Solution:
  • Hyperparameter Optimization: Use formal hyperparameter tuning strategies.
    • For smaller compute budgets, use Bayesian Optimization to make informed sequential decisions [42].
    • For large jobs, use the Hyperband strategy with early stopping to reduce computation time [42].
    • Use Random Search to run a large number of parallel jobs if subsequent runs do not depend on prior results [42].
  • Consider Alternatives: For variable selection, if Lasso (which uses a single penalty) is unstable, consider using severe data reduction (like sparse principal components) followed by ordinary modeling, or Bayesian ridge regression with posterior selection [40].

Frequently Asked Questions (FAQs)

FAQ 1: What is the fundamental trade-off when setting a penalty parameter?

The penalty parameter directly balances optimality versus feasibility [43] [3]. A lower parameter prioritizes reducing the original objective function f(x), even if it means accepting some constraint violation. A higher parameter prioritizes satisfying the constraints, which can lead to a solution that is feasible but may have a worse objective value. The goal is to find a parameter that achieves a satisfactory balance for your specific application.

FAQ 2: Are there automated methods for penalty parameter selection?

Yes, recent research has developed methods that automate this process. One advanced approach involves solving the underlying optimization problem and tuning its associated penalty hyperparameters simultaneously within a single algorithm [41]. Another method uses a self-supervised, penalty-based loss function to learn a mapping for robust constrained optimization, effectively automating the balance between sub-optimality and feasibility [43].

FAQ 3: What is the difference between a penalty method and an augmented Lagrangian method?

Both methods transform a constrained problem into an unconstrained one. However, a key drawback of the basic penalty method is that it requires the penalty parameter to go to infinity to recover an exact solution, which makes the problem ill-conditioned [6]. Augmented Lagrangian methods are a more advanced class of penalty methods that incorporate Lagrange multiplier estimates. This allows them to converge to exact solutions without needing to drive the penalty parameter to infinity, making the unconstrained subproblems easier to solve numerically [6].

Experimental Protocols & Data

Protocol 1: Adaptive Penalty Parameter Update for Stochastic Optimization

This protocol is based on a method for stochastic equality-constrained problems [39].

• Initialization: Choose an initial penalty parameter ρ₀, a growth factor β > 1 (e.g., 10), and a tolerance Ï„ for constraint violation.
• Subproblem Solution: At iteration k, approximately solve the unconstrained penalized problem min f(x) + ρₖ * Penalty(c(x)) using a truncated stochastic prox-linear algorithm.
• Constraint Check: Evaluate the constraint violation ||c(xâ‚–)||.
• Parameter Update: If the constraint violation is above the tolerance Ï„, increase the penalty parameter: ρₖ₊₁ = β * ρₖ. Otherwise, keep it constant: ρₖ₊₁ = ρₖ.
• Termination: The method is designed to terminate after finitely many iterations. An approximate stationary point of the penalty function then corresponds to an approximate KKT point of the original constrained problem [39].

Protocol 2: Tuning Elastic Net Hyperparameters via Cross-Validation

This protocol details the steps for tuning the two parameters in the Elastic Net penalty, which combines L1 (Lasso) and L2 (Ridge) penalties [42].

• Define Grid: Create a two-dimensional grid of candidate values for the mixing parameter α (between 0 and 1) and the overall penalty strength λ.
• Choose Strategy: Select a hyperparameter tuning strategy suitable for your computational resources.
  • Bayesian Optimization: Efficient for sequential evaluations with a limited budget.
  • Random Search: Efficient for running many parallel jobs.
  • Grid Search: Methodically searches the entire grid but is computationally intensive.
• Cross-Validate: For each (α, λ) pair, perform cross-validation (e.g., 5-fold or 10-fold) to estimate the model's generalization error.
• Select Best: Choose the hyperparameter pair that gives the lowest cross-validation error.
• Stability Check (Optional): To assess the reliability of the selected features, bootstrap the entire process (data sampling and model tuning) and check the consistency of the selected features across bootstrap samples [40].

Diagram 1: Elastic Net hyperparameter tuning workflow.

Table 1: Oracle Complexity for Finding an ϵ-KKT Point

The following table summarizes the computational complexity of a proposed stochastic penalty method, measured in the number of required stochastic evaluations [39].

Stochastic Evaluation Type	Complexity Order	Note
Gradient Evaluations	O(ϵ⁻³)	For the objective and constraints
Function Evaluations	O(ϵ⁻⁵)	For the constraints only

The Scientist's Toolkit

Table 2: Key Research Reagent Solutions

Item	Function in Optimization
Stochastic Prox-Linear Algorithm	An algorithm used to approximately solve the unconstrained penalty subproblems in stochastic optimization. It handles the non-smoothness introduced by the penalty function [39].
Hyperparameter Optimization Library	Software tools (e.g., from AWS SageMaker, Weka, scikit-learn) that implement strategies like Bayesian Optimization, Random Search, and Hyperband to automate the search for optimal penalty parameters [42].
Quadratic Penalty Function	A common penalty function of the form g(c(x)) = max(0, c(x))². It penalizes constraint violations smoothly and is widely used for its differentiability properties [6].
Exact Penalty Function	A type of penalty function (often using an L1 norm) for which an exact solution to the constrained problem can be recovered for a finite penalty parameter, avoiding ill-conditioning [39] [6].
Modeling Language/System	Software (e.g., AMPL, GAMS, Pyomo) that helps formulate the optimization model in symbolic terms, interface with various solvers, and analyze results, simplifying the implementation of penalty methods [44].

Dynamic and Adaptive Penalty Strategies for Evolutionary Algorithms

Troubleshooting Guide: Frequently Asked Questions

Q1: My algorithm is converging to infeasible solutions. How can I adjust my penalty strategy?

This common issue often stems from an imbalance between penalty pressure and objective function optimization.

• Diagnosis: The penalty coefficients are likely too weak, causing the algorithm to ignore constraints and favor regions with good objective function values but high constraint violation.
• Solution: Implement an adaptive penalty function that increases pressure over time. For example, use a function that considers the satisfaction rate and total constraint deviations, not just the objective value [32]. A co-evolutionary approach can also auto-construct effective perturbation logics and penalty adjustments tailored to the problem [45].
• Protocol:
  • Initialize with a low penalty coefficient.
  • Monitor the proportion of feasible individuals in the population (feas_ratio).
  • If feas_ratio is below a target threshold (e.g., 5%) for a set number of generations, increase the penalty coefficient multiplicatively.
  • Re-evaluate the population with the new penalty function.

Q2: The algorithm is prematurely converging to a suboptimal, albeit feasible, region. What should I do?

This indicates excessive penalty pressure or poor diversity management, causing a loss of promising infeasible solutions near the feasible region boundary.

• Diagnosis: The penalty function is likely too aggressive or lacks mechanisms to exploit useful information from infeasible solutions.
• Solution:
  • Introduce a dynamic or ε-constraint method that relaxes constraints in early generations to allow exploration near boundaries [46].
  • Use a multi-objective approach to treat constraint violation as a separate objective, preserving a diverse set of solutions [46].
  • Employ a feasibility rule that strictly prefers feasible over infeasible solutions but uses a stochastic ranking to compare infeasible ones based on both objective and constraint violation [46].
• Protocol for ε-constraint:
  • Start with a large ε value to tolerate a high degree of constraint violation.
  • Gradually reduce ε to zero according to a predefined schedule (e.g., linear or exponential decay) as generations proceed.
  • This guides the population from the infeasible region toward the feasible global optimum.

Q3: How do I handle problems where the global optimum lies on a narrow feasible boundary?

This is a complex scenario where traditional penalty methods often fail.

• Diagnosis: Standard penalties may struggle to precisely locate and converge onto a very small feasible region.
• Solution: A hybrid constraint handling technique is recommended. Combine a feasibility rule with a local search operator or a repair strategy for infeasible solutions [46].
• Protocol for Random Direction Repair (RDR):
  • For an infeasible solution, generate a set of random search directions.
  • Evaluate the constraint violation after taking a small step in each direction.
  • Move the solution in the direction that most reduces the constraint violation.
  • This requires only a small number of additional fitness evaluations but can significantly aid in crossing feasibility gaps [46].

Q4: My constrained optimization is computationally expensive. How can I improve efficiency?

The overhead of evaluating constraints for every candidate solution can be a major bottleneck.

• Diagnosis: The algorithm is performing unnecessary evaluations without learning from past searches.
• Solution:
  • Use a memory-based mechanism, inspired by Tabu Search, to avoid re-evaluating similar solutions or to store and reuse the best-found solutions [32].
  • Implement surrogate models (meta-models) to approximate constraint functions for most individuals, reserving exact evaluations only for the most promising candidates [45].
• Protocol for Memory-Based Evaluation:
  • Maintain an archive of recently visited solutions and their fitness/constraint values.
  • Before evaluating a new solution, check its similarity (e.g., Euclidean distance) to solutions in the archive.
  • If a sufficiently similar solution is found, approximate its fitness and constraint values from the archive, avoiding a full function evaluation.

Experimental Protocols for Validating Penalty Strategies

To ensure your adaptive penalty strategy is effective, validate it against standardized benchmarks and metrics.

Protocol 1: Benchmarking on Engineering Design Problems

This protocol tests the algorithm's performance on well-known, real-world constrained problems.

• Objective: Compare the performance of a new adaptive penalty algorithm against state-of-the-art methods.
• Benchmarks: Use classic engineering problems such as the Welded Beam Design, Pressure Vessel Design, and Tension/Compression Spring Design [32] [45].
• Methodology:
  • Run the proposed algorithm (e.g., a penalty-based algorithm or a co-evolutionary algorithm) a minimum of 30 independent times on each benchmark problem to account for stochasticity.
  • Record the best solution, mean solution, standard deviation, and the number of function evaluations required to reach a feasible solution.
  • Compare these results with those obtained by other algorithms from the literature (e.g., UDE, TPDE, ε-DE) using the same benchmarks [46] [32].
• Success Metrics: The algorithm should consistently find the known global optimum or a competitive solution with high reliability and efficiency.

Protocol 2: Evaluation on the CEC 2017 Constrained Optimization Benchmark

This provides a modern and rigorous test suite.

• Objective: Assess scalability and performance on a diverse set of constrained functions.
• Benchmarks: The CEC 2017 benchmark suite for constrained optimization [45].
• Methodology:
  • Follow the official CEC 2017 competition guidelines for experimental setup, including maximum function evaluations.
  • Compare the proposed algorithm's ranking against other participants in the competition or published results.
  • Perform statistical tests, such as the Wilcoxon signed-rank test, to confirm the significance of performance differences [47].
• Success Metrics: Achieving a top rank in the benchmark comparison and demonstrating statistically superior or equivalent performance to other state-of-the-art algorithms.

Comparative Analysis of Penalty Strategies

The table below summarizes key penalty strategies discussed in recent literature to aid in selection.

Table 1: Comparison of Constraint Handling Techniques for Evolutionary Algorithms

Strategy Type	Core Mechanism	Key Advantages	Common Challenges
Adaptive Penalty [32] [45]	Automatically adjusts penalty coefficients based on evolutionary feedback (e.g., feasible ratio).	Reduces need for manual parameter tuning; adapts to problem landscape.	Risk of premature convergence if adaptation is too aggressive.
Feasibility Rules [46]	Strictly prefers feasible over infeasible solutions; uses objective value for ties.	Simple to implement; very effective when feasible region is reasonably large.	Can be too greedy, rejecting useful infeasible solutions near the boundary.
ε-Constraint [46]	Allows tolerance (ε) for constraint violation, which is decreased over time.	Excellent for locating optima on feasibility boundaries; guides search effectively.	Performance sensitive to the chosen ε-reduction schedule.
Multi-Objective [46]	Treats constraints as separate objectives to be minimized.	No need to define penalty coefficients; inherently maintains diversity.	Can be computationally expensive; may struggle if the Pareto front is complex.
Stochastic Ranking [46]	Uses a probability P to decide whether to rank by objective or constraint violation.	Balances objective and constraint information effectively.	Performance depends on the choice of the probability parameter P.
Co-evolutionary & Hybrid [46] [45]	Co-evolves solutions and strategies, or combines multiple techniques.	Highly adaptive; can automatically adjust its search logic to the problem.	Increased algorithmic complexity; potentially higher computational cost.

Workflow Visualization

The following diagram illustrates the logical structure of a robust adaptive penalty algorithm, integrating multiple strategies from the troubleshooting guide.

The Scientist's Toolkit: Research Reagent Solutions

Table 2: Essential Computational Tools for Evolutionary Constrained Optimization

Tool / Component	Function in Experimentation	Key Considerations
CEC Benchmark Suites (e.g., CEC 2017)	Provides a standardized set of constrained problems for fair and reproducible comparison of algorithms [45].	Ensure implementation matches the official technical report precisely.
Adaptive Penalty Function	A core "reagent" that automatically adjusts constraint pressure, reducing manual tuning [32] [45].	Design based on population statistics (e.g., feasible ratio, constraint violation variance).
Local Search / Repair Operator (e.g., LEO, RDR)	Acts as a "catalyst" to refine solutions, escape local optima, and repair infeasible candidates [46] [47].	Balance the computational cost of the operator with the quality improvement it provides.
Co-evolutionary Framework	A "scaffold" that allows for the simultaneous evolution of solutions and their perturbation strategies [45].	Increases complexity but offers high adaptability for black-box problems.
Statistical Testing Suite (e.g., Wilcoxon, Friedman)	The "analytical instrument" for rigorously validating that performance improvements are statistically significant [47].	A p-value < 0.05 is typically required to reject the null hypothesis of equal performance.

Handling Non-Differentiability in L1 and Exact Penalty Functions

Frequently Asked Questions

FAQ 1: What causes non-differentiability in exact penalty functions, and why does it matter for my optimization algorithm?

Non-differentiability arises from the mathematical operations used to handle constraint violations. The L₁ penalty function sums the absolute values of equality constraint violations and the magnitudes of inequality constraint violations, defined as P₁(x) = f(x) + ρ Σ|hᵢ(x)| + ρ Σ max(0, gⱼ(x)) [48]. The L∞ penalty function uses the maximum violation across all constraints: P∞(x) = f(x) + ρ max{|hᵢ(x)|, max{0, gⱼ(x)}} [48]. These max and absolute value operations create points of non-differentiability wherever constraints are exactly satisfied (háµ¢(x) = 0 or gâ±¼(x) = 0) [48] [19]. This is significant because most standard optimization algorithms require gradient information to efficiently find minima. When derivatives do not exist at these critical points, algorithms may fail to converge or experience numerical instability.

FAQ 2: My optimization is converging slowly or "chattering" near the solution. Is this related to non-differentiability?

Yes, this is a classic symptom. When an algorithm based on smooth derivatives (like gradient descent) encounters a non-differentiable point, it cannot reliably determine a descent direction, often causing it to oscillate or "chatter" around the optimum [19]. This behavior is particularly pronounced with exact penalty functions because the solution of the original constrained problem often lies precisely at the point of non-differentiability. The algorithm struggles to settle at a point where the objective and penalty terms are balanced, leading to slow convergence and imprecise results.

FAQ 3: Are there smooth alternatives to the L₁ penalty function that still provide exact solutions?

Yes, recent research has developed smooth exact penalty functions. One approach involves creating a "differentiating active function" inspired by topology optimization principles [19]. This function uses a smooth, tunable function to indicate the presence of a constraint violation, effectively creating a smooth bridge between the feasible and infeasible regions. Another method introduces an additional variable or uses special smoothing functions like the Huber function to approximate the L₁ penalty [19]. While these can eliminate numerical instability, they may require higher-order derivative evaluations or complicate the objective function [19].

FAQ 4: How can I verify that a candidate solution from a non-differentiable optimizer is truly a minimum?

For non-differentiable functions, the standard Karush-Kuhn-Tucker (KKT) conditions are replaced by more general optimality conditions. You should check the subgradient optimality condition: a point x* is a minimum if there exists a subgradient ∂P₁(x*) such that 0 ∈ ∂P₁(x*) [48]. In practice, this means verifying that for small perturbations in any direction, the function value does not decrease. Furthermore, you can check that the candidate solution satisfies the constraints of your original problem to within a acceptable tolerance, confirming that the penalty function has achieved its goal [48] [19].

Troubleshooting Guides

Problem: Algorithm fails to converge or terminates with a numerical error.

This is common when using gradient-based methods on non-smooth penalty functions [19].

• Step 1: Switch to a non-smooth optimizer. Use algorithms specifically designed for non-differentiable problems.

  • Subgradient Methods: These generalize gradient descent by using subgradients instead of gradients. However, they typically have slower convergence [48].
  • Bundle Methods: These accumulate subgradient information from previous iterations to build a model of the function, leading to more robust convergence for convex problems [48].

• Step 2: Implement a smoothing technique. Approximate the non-smooth penalty function with a smooth one.

  • Moreau-Yosida Regularization: This adds a quadratic term to the penalty function, making it strongly convex and smooth [48].
  • Log-Sum-Exp Approximation: The max operation in the L∞ penalty can be approximated using a smooth log-sum-exp function: max(a, b) ≈ (1/μ) * log(exp(μ*a) + exp(μ*b)), where μ is a smoothing parameter [48].

• Step 3: Check the penalty parameter. If the penalty parameter ρ is too large, the problem becomes ill-conditioned, causing numerical errors even with smoothing. Start with a moderate ρ and increase it gradually [6].

Problem: Solution is infeasible or has significant constraint violation.

This indicates that the penalty parameter is not sufficiently large to enforce the constraints exactly [48].

• Step 1: Check the theoretical exactness condition. Exact penalty functions like L₁ and L∞ are guaranteed to produce an exact solution only if the penalty parameter ρ exceeds a specific threshold ρ*, which is related to the magnitude of the optimal Lagrange multipliers of the original constrained problem [48] [19].

• Step 2: Increase the penalty parameter strategically. Use an adaptive strategy: begin with a small ρ, find the unconstrained minimum, then increase ρ and use the previous solution as a new starting point. Repeat until constraints are satisfied within the desired tolerance [6].

• Step 3: Use a merit function. Employ a merit function to monitor progress, which combines the objective function reduction and constraint violation into a single scalar value. This helps ensure that each step of the algorithm moves toward both optimality and feasibility [48].

Problem: Inconsistent results with different starting points.

Non-differentiable problems can have multiple local minima, and different starting points may lead to different local solutions.

• Step 1: Employ a multi-start strategy. Run the optimization algorithm from a diverse set of initial points and compare the objective function values and feasibility of the resulting solutions. This helps identify the global optimum or a better local optimum.

• Step 2: Verify constraint qualifications. The existence of an exact penalty parameter and the reliability of the method can depend on certain conditions being met, such as the Linear Independent Constraint Qualification (LICQ) or the Mangasarian-Fromovitz Constraint Qualification (MFCQ) [19]. Ensure your problem satisfies these.

• Step 3: Consider a hybrid approach. Start with a smooth penalty function or an augmented Lagrangian method to get near the solution, then switch to an exact L₁ penalty function for a final, high-precision solve [48] [19].

Comparison of Numerical Methods for Non-Differentiable Problems

The table below summarizes key algorithms for handling non-differentiability in exact penalty functions.

Method	Key Mechanism	Convergence Rate	Advantages	Disadvantages
Subgradient Method [48]	Uses subgradients (generalized gradients) for descent direction.	Slow (typically sublinear)	Simple to implement; guaranteed convergence for convex problems.	Sensitive to step size; can be very slow in practice.
Bundle Method [48]	Builds a piecewise linear model of the function using past subgradients.	Slow to medium (linear for convex)	More stable than subgradient; keeps a history of information.	Higher memory and computational cost per iteration.
Smoothing Method [48] [19]	Approximates the non-smooth function with a smooth one.	Fast (superlinear/quadratic if using Newton)	Enables use of fast, smooth optimizers (e.g., SQP, Newton).	Solution is an approximation; may require careful tuning of smoothing parameter.
Augmented Lagrangian Method (ALM) [48]	Combines penalty with Lagrange multipliers.	Fast (typically superlinear)	Avoids ill-conditioning from large penalty parameters; exact with finite penalty.	Introduces dual variables, increasing problem dimension.

Experimental Protocol: Implementing and Testing a Smoothing Function for L₁ Penalty

This protocol details the methodology for creating and benchmarking a smoothed version of the L₁ exact penalty function, suitable for use with gradient-based solvers.

1. Background and Purpose The non-differentiability of the L₁ penalty function at constraint boundaries hinders the use of efficient gradient-based optimizers. This experiment aims to implement a smooth approximation, evaluate its accuracy, and benchmark its performance against a standard non-smooth optimizer.

2. Reagents and Computational Tools

• Software: Python (with NumPy, SciPy, and ADOL-C for automatic differentiation) or MATLAB.
• Optimization Problem: A standard test problem from the CUTEst collection, featuring both equality and inequality constraints.
• Algorithms for Comparison:
  • Experimental Method: A gradient-based algorithm (e.g., BFGS) applied to the smoothed L₁ penalty.
  • Control Method: A subgradient algorithm applied to the original L₁ penalty function.

3. Step-by-Step Procedure

• Step 1: Problem Formulation. Define your constrained optimization problem: min f(x) subject to háµ¢(x) = 0, gⱼ(x) ≤ 0.
• Step 2: Smooth Function Implementation. Replace the non-differentiable max and abs functions. A common choice is the Huber function for inequality constraints:
  • For an inequality constraint g(x) ≤ 0, the penalty term max(0, g(x)) is replaced with:
    • (g(x) - ε/2) if g(x) > ε
    • (g(x))² / (2ε) if 0 < g(x) ≤ ε
    • 0 if g(x) ≤ 0
  • Here, ε > 0 is a smoothing parameter that controls the accuracy of the approximation [19].
• Step 3: Parameter Tuning. Systematically vary the smoothing parameter ε and the penalty parameter ρ. A common strategy is to decrease ε gradually in a series of solves to improve accuracy.
• Step 4: Optimization Run. For each (ρ, ε) pair, use a gradient-based optimizer to minimize the smoothed penalty function. Record the final solution, number of iterations, and function evaluations.
• Step 5: Control Experiment. Solve the same problem using a subgradient method on the original, non-smooth L₁ penalty function.
• Step 6: Performance Metrics. Compare the results based on:
  • Final Objective Value (f(x))
  • Constraint Violation: Σ|hᵢ(x)| + Σ max(0, gⱼ(x))
  • Computational Cost: Total CPU time and number of iterations to convergence.

The Scientist's Toolkit: Research Reagent Solutions

Item Name	Function / Role in Experiment
L₁ Exact Penalty Function [48]	The core objective function for transforming a constrained problem into an unconstrained one. It guarantees exactness for a sufficiently large penalty parameter.
Subgradient Optimizer [48]	A solver algorithm designed to handle non-differentiable problems directly by generalizing the concept of a gradient.
Smoothing Parameter (ε) [19]	A tunable numerical value that controls the trade-off between the accuracy of the smooth approximation and its differentiability. A smaller ε yields a more accurate but steeper function.
Huber Loss Function [19]	A specific smooth function used to approximate the non-differentiable max(0, g(x)) operation for inequality constraints, behaving quadratically near zero and linearly farther away.
Merit Function [48]	A monitoring function used in line-search algorithms to ensure that each step improves both optimality and feasibility, preventing divergence.
Penalty Parameter (ρ) [48]	A scaling factor that determines the weight of the constraint violation penalty relative to the original objective function.

Workflow Diagram: Handling Non-Differentiability

The diagram below illustrates a logical workflow for choosing an appropriate strategy when facing non-differentiability in L₁ exact penalty functions.

Balancing Multiple Objectives and Constraints in Molecular Optimization

Frequently Asked Questions (FAQs)

FAQ 1: What makes constrained multi-objective molecular optimization different from standard optimization?

Standard molecular optimization often focuses on improving a single property (like logP or QED) or uses a weighted sum to combine multiple properties. In contrast, constrained multi-objective optimization treats each property as a separate objective and incorporates strict, drug-like criteria as constraints that must be satisfied. This is crucial because it finds molecules that not only have a good balance of multiple desired properties but also adhere to essential real-world requirements like synthesizability or specific structural features. This approach is more complex because constraints can make the feasible molecular space narrow, disconnected, and irregular [29] [28].

FAQ 2: My optimization run is converging on infeasible molecules with great properties. How can I guide it back to the feasible region?

This is a common challenge where the algorithm is overly focused on property optimization and ignores constraints. The CMOMO framework addresses this with a dynamic constraint handling strategy. It splits the optimization into two scenarios [29] [28]:

• Unconstrained Scenario: The algorithm first explores the search space widely to find molecules with good convergence and diversity in their properties, temporarily ignoring constraints.
• Constrained Scenario: The algorithm then switches to a mode that uses a ranking aggregation strategy to evaluate and select molecules based on both their property values and their constraint satisfaction, effectively balancing the two aspects.

FAQ 3: What are the main types of penalty functions used in optimization?

The literature describes several classes of penalty functions for handling constraints, each with different characteristics and applications. The table below summarizes the main types.

Penalty Function Type	Key Feature	Typical Use Case
Standard Objective Penalty [4]	Aggregates constraint violations into the objective function. A constraint penalty factor (ρ) controls the penalty strength.	Finding local optimal solutions to constrained problems.
Exact Penalty [49] [50]	For a finite penalty parameter value, solutions to the penalized problem are also solutions to the original constrained problem.	Solving a single unconstrained problem instead of a sequence of problems; useful for large-scale or non-convex problems.
Filled Penalty [4]	Designed to escape local optima; can find a solution that is better than a given local optimum.	Finding globally approximate optimal solutions in a finite number of steps.

FAQ 4: How can I ensure my generated molecules are synthetically accessible?

While simple scoring functions (like SA-Score) offer a rough estimate, a more robust approach is to integrate reaction-aware generation directly into the optimization process. The TRACER framework uses a conditional transformer model trained on chemical reaction data (SMILES sequences of reactants and products). When paired with an optimization algorithm like Monte Carlo Tree Search (MCTS), it can generate molecules along with plausible synthetic pathways, ensuring that the proposed structures are based on known chemical transformations [51]. Using reaction templates as conditional tokens significantly improves the model's accuracy in proposing realistic products [51].

Troubleshooting Guides

Problem: Poor Performance in High-Dimensional Chemical Space Issue: The optimization algorithm struggles to efficiently search the vast chemical space and generate valid, high-quality molecules. Solution: Implement a cooperative search strategy between discrete chemical space and a continuous latent (implicit) space.

• Methodology: Use a pre-trained variational autoencoder (VAE) or similar model to encode molecules into continuous vectors [29] [28].
• Perform evolutionary operations (like crossover and mutation) in this continuous latent space. This allows for smoother and more efficient exploration.
• Decode the resulting vectors back into molecular structures (SMILES) for property evaluation.
• Strategy Enhancement: The Vector Fragmentation-based Evolutionary Reproduction (VFER) strategy can be used to enhance the efficiency of generating offspring in the latent space [29] [28].

Problem: Penalty Function Method Fails to Find Feasible Solutions Issue: The algorithm fails to find molecules that satisfy all constraints, even after many iterations. Solution: Diagnose and adjust the constraint handling mechanism.

• Verify Constraint Formulation: Ensure your constraints are correctly formulated and measurable for every generated molecule. Use a Constraint Violation (CV) function to quantify the violation degree for each molecule. A CV of zero indicates a feasible molecule [28].
• Check Penalty Parameters: If using a penalty function method, the value of the penalty parameter ρ is critical. If ρ is too small, the algorithm may ignore constraints. Systematically increase ρ or consider adaptive penalty strategies [4].
• Switch to a Dynamic Strategy: If static penalties fail, implement a dynamic strategy like in CMOMO, which first focuses on finding high-performance molecules (ignoring constraints) and then shifts focus to satisfying constraints without sacrificing too much performance [29] [28].

Problem: Algorithm Is Stuck in a Local Optimum Issue: The optimization converges to a suboptimal set of molecules and fails to improve further. Solution: Employ strategies to enhance global exploration.

• Maintain Population Diversity: Use multi-objective algorithms like NSGA-II for environmental selection, which preserve both convergence towards optimal properties and diversity in the molecular population [29].
• Quality Initialization: Start the optimization from a high-quality and diverse initial population. This can be done by performing linear crossover between the latent vector of your lead molecule and latent vectors of similar, high-property molecules from a public database [29] [28].
• Consider Filled Penalty Functions: For local optima issues in penalty-based methods, investigate filled penalty functions, which are specifically designed to "fill" the basin of local optima, allowing the search to escape and find a better solution [4].

The Scientist's Toolkit: Research Reagent Solutions

The following table details key computational tools and resources used in advanced molecular optimization experiments.

Resource / Tool	Function in the Experiment
Pre-trained Molecular Encoder/Decoder [29] [28]	Maps molecules between discrete chemical structures (SMILES) and a continuous latent vector space, enabling efficient evolutionary operations.
Bank Library [29] [28]	A custom database of high-property molecules similar to the lead compound. Used to generate a high-quality, diverse initial population for the optimization.
RDKit	An open-source cheminformatics toolkit. Used for critical tasks such as validity verification of decoded SMILES strings, calculation of molecular descriptors, and substructure matching for constraint checks [28].
Reaction Database (e.g., USPTO) [51]	A dataset of known chemical reactions. Used to train conditional transformer models (like in TRACER) to ensure generated molecules are synthetically accessible.
Quantitative Structure-Activity Relationship (QSAR) Model [51]	A predictive model that maps molecular structures to biological activity or other properties. Serves as the objective function for optimization in lieu of physical assays during in silico screening.

Experimental Protocol: Dynamic Cooperative Multi-Objective Optimization (CMOMO)

This protocol outlines the key methodology for performing constrained multi-property molecular optimization using the CMOMO framework [29] [28].

1. Problem Formulation

• Define Objectives: Specify the molecular properties to be optimized (e.g., QED, PlogP, bioactivity). These are your objective functions ( f1(x), f2(x), ..., f_k(x) ).
• Define Constraints: Specify the drug-like criteria (e.g., ring size, presence/absence of certain substructures) as inequality constraints ( g_j(x) \leq 0 ).

2. Population Initialization

• Input: A lead molecule (SMILES string).
• Construct a Bank Library: Gather molecules from public databases (e.g., ChEMBL, PubChem) that are structurally similar to the lead and have high property values.
• Encode Molecules: Use a pre-trained molecular encoder to convert the lead molecule and all molecules in the Bank library into latent vectors ( z ) in a continuous space.
• Generate Initial Population: Perform linear crossover between the latent vector of the lead molecule and the vectors from the Bank library to create an initial population of latent vectors ( P_0 ).

3. Dynamic Cooperative Optimization This phase involves iterative cycles of reproduction, evaluation, and selection, coordinating between the continuous latent space and discrete molecular space.

Diagram 1: CMOMO dynamic cooperative optimization workflow.

• Unconstrained Optimization Phase:

  • Step 3.1: Evolutionary Reproduction (VFER): Apply the Vector Fragmentation-based Evolutionary Reproduction strategy to the current population ( Pt ) to generate offspring population ( Ot ) in the latent space [29] [28].
  • Step 3.2: Decoding and Evaluation: Decode all latent vectors in ( Pt ) and ( Ot ) to SMILES strings using a pre-trained decoder. Filter out invalid molecules with RDKit. Evaluate the multiple objective properties for each valid molecule. At this stage, constraints are not considered.
  • Step 3.3: Environmental Selection: Combine parent and offspring populations. Use the non-dominated sorting and crowding distance selection from the NSGA-II algorithm to select the best molecules for the next generation ( P_{t+1} ) based solely on their property values [29].
  • Step 3.4: Iterate: Repeat steps 3.1-3.3 for a predefined number of generations to explore the search space for high-performance molecules.

• Constrained Optimization Phase:

  • Step 3.5: Switch Scenario and Repeat Reproduction: Switch the algorithm's mode to the constrained scenario. Continue using VFER to generate offspring.
  • Step 3.6: Constraint-Aware Evaluation: Decode and evaluate molecules as before, but now also calculate the Constraint Violation (CV) for each molecule using the formula: [ CV(x) = \sum{j=1}^{m} [\max(0, \, gj(x))]^2 ] A molecule is feasible if ( CV(x) = 0 ) [28].
  • Step 3.7: Feasibility-Promoting Selection: Use a ranking aggregation strategy that prioritizes:
    • Feasible molecules over infeasible ones.
    • Among feasible molecules, those with better non-domination ranks and diversity.
    • Among infeasible molecules, those with smaller constraint violations and better properties [29].
  • Step 3.8: Final Iteration: Repeat steps 3.5-3.7 until the overall stopping criteria are met (e.g., total number of iterations).

4. Output The final output is a set of non-dominated molecules that are either feasible or have very low constraint violations, representing the best trade-offs between the multiple optimized properties.

Evaluating Performance: Benchmarking and Comparisons with Alternative Methods

Frequently Asked Questions

1. What are the major sources of discrepancy between predicted and experimentally measured bioactivities? Discrepancies often arise from data quality and modeling challenges. Key sources include:

• Model Applicability Domain: Predictions are less reliable for compounds with chemical structures highly dissimilar to those in the training data.
• Assay Noise and Variability: Biological noise in the experimental validation assay can obscure the true signal.
• Feature Representation: The choice of molecular descriptors (e.g., chemical fingerprints, morphological profiles) may not fully capture the biological activity in the relevant context [52] [53].

2. How can I improve the concordance between my computational predictions and experimental results?

• Utilize Multi-Modal Data: Combine chemical structure data with phenotypic profiles (e.g., from Cell Painting or gene expression assays) to create more robust models. Research shows that combining chemical structures with morphological profiles can predict up to 3 times more assays accurately than using chemical structures alone [53].
• Implement Rigorous Validation: Use scaffold-based splits during model training to ensure you are testing on structurally novel compounds, which provides a more realistic estimate of model performance [53] [54].
• Optimize Hit Identification Strategy: For phenotypic profiling data, multi-concentration analysis approaches (like feature-level or category-based curve-fitting) generally detect more true active hits with a controlled false positive rate compared to single-concentration methods [52].

3. My model performed well during cross-validation but failed in experimental testing. What happened? This often indicates overfitting or data leakage. Ensure that your training and test sets are properly separated, especially when dealing with multiple bioactivity readings for the same compound or highly similar compounds. The validation protocol must avoid any information leakage between the training and validation data to realistically assess the model's predictive power for novel compounds [54].

4. Which machine learning model is best for predicting bioactivity? No single model is universally best. The choice depends on your data and goal. However, kernel-based learning algorithms (like KronRLS) have demonstrated success in predicting drug-target interactions, achieving high correlation (e.g., 0.77) with experimentally measured binding affinities in rigorous tests [54]. Other models, including those based on graph convolutional networks for chemical structures, have also shown strong performance [53].

Experimental Protocols for Validation

Protocol 1: Computational-Experimental Framework for Drug-Target Interaction Validation

This protocol outlines a systematic approach for predicting and verifying compound-target bioactivities, based on a validated, kernel-based method [54].

Step	Description	Key Considerations
1. Data Preparation	Gather chemical structures (e.g., SMILES) and protein target sequences. Compile a training set of known bioactivities (e.g., Ki, IC50).	Ensure data quality and consistency. Use standardized formats.
2. Model Training	Compute molecular descriptors (kernels) for drugs and proteins. Train a regression model (e.g., KronRLS) to predict binding affinities.	Kernel choice is critical; consider extended target-profile kernels [54].
3. Prediction	Use the trained model to predict unmeasured bioactivities for compound-target pairs of interest.	Differentiate between "Bioactivity Imputation" and "New Drug" prediction scenarios [54].
4. Experimental Validation	Select top predictions for laboratory testing. Use standardized in vitro binding assays (e.g., kinase profiling panels).	Test a sufficient number of predictions (e.g., 100 pairs) to statistically validate correlation [54].
5. Correlation Analysis	Calculate correlation coefficients (e.g., Pearson) between predicted and measured bioactivities.	A high correlation (e.g., >0.75) indicates strong predictive power [54].

Protocol 2: Hit Identification in Phenotypic Profiling Assays

This protocol describes strategies for identifying active compounds ("hits") in high-content imaging assays like Cell Painting, which can be used for validation [52].

Step	Description	Method Variants
1. Feature Extraction	Extract hundreds to thousands of morphological features from cell images.	CellPainting assay typically yields ~1,300 features [52].
2. Data Normalization	Normalize well-level data to solvent controls using robust methods like Median Absolute Deviation (MAD).	Z-score standardization based on solvent control SD is also common [52].
3. Hit Identification	Apply a hit-calling strategy to distinguish active from inactive treatments.	- Multi-concentration: Feature-level, category-based, or global curve-fitting.- Single-concentration: Signal strength or profile correlation among replicates [52].
4. Potency Estimation	Calculate a Phenotype-Altering Concentration (PAC), defined as the median potency of the most sensitive responsive category.	For a higher-actives chemical set, a permissive Benchmark Response (1 SD) may be appropriate [52].

The table below consolidates key performance metrics from cited studies to serve as a benchmark for your own work.

Study	Data Modality / Method	Key Performance Metric	Result	Experimental Context
Cichonska et al. [54]	Kernel-based model (KronRLS)	Correlation (predicted vs. measured bioactivity)	0.77 (p < 0.0001)	Validation of 100 predicted compound-kinase pairs
Cichonska et al. [54]	Kernel-based model (KronRLS)	Experimentally validated off-targets	4 out of 7	Case study on the kinase inhibitor Tivozanib
Arevalo et al. [53]	Chemical Structure (CS) alone	Number of well-predicted assays (AUROC > 0.9)	16 assays	Prediction across 270 diverse bioactivity assays
Arevalo et al. [53]	Cell Painting (MO) alone	Number of well-predicted assays (AUROC > 0.9)	28 assays	Prediction across 270 diverse bioactivity assays
Arevalo et al. [53]	CS + MO (Late Fusion)	Number of well-predicted assays (AUROC > 0.9)	31 assays	Prediction across 270 diverse bioactivity assays

Workflow and Relationship Visualizations

Bioactivity Validation Workflow

Multi-Modal Data Fusion

The Scientist's Toolkit: Research Reagent Solutions

Item	Function in Experimental Validation
U-2 OS Cell Line	A human osteosarcoma cell line commonly used in phenotypic profiling assays like Cell Painting to assess morphological changes [52].
Cell Painting Assay Kits	A set of fluorescent dyes used to stain major cellular compartments (nucleus, nucleoli, ER, Golgi, cytoskeleton, mitochondria), enabling untargeted morphological profiling [52] [53].
L1000 Assay	A high-throughput gene expression profiling technology that measures the transcriptomic response of cells to compound treatment, providing another rich data modality [53].
Kinase Profiling Panels	Commercial services (e.g., from DiscoverX, Millipore) that provide in vitro testing of compound activity across a wide range of kinase targets, ideal for validating predicted drug-target interactions [54].
KronRLS Algorithm	A kernel-based regularized least-squares machine learning algorithm proven effective for predicting continuous binding affinity values in drug-target interaction studies [54].
BMDExpress Software	A computational tool for performing benchmark dose (BMD) analysis and concentration-response modeling on high-throughput screening data, useful for hit identification [52].

Frequently Asked Questions (FAQs)

FAQ 1: What is the fundamental difference in how penalty, barrier, and augmented Lagrangian methods handle constraints?

Penalty methods transform a constrained problem into a series of unconstrained problems by adding a term to the objective function that penalizes constraint violations. The penalty parameter is increased over iterations to force the solution towards feasibility [6]. Barrier methods also use a series of unconstrained problems, but they force the solution to remain strictly inside the feasible region by using a barrier function whose value increases to infinity as the solution approaches the boundary of the feasible set [55]. Augmented Lagrangian methods add both a penalty term and an additional term designed to mimic a Lagrange multiplier, which helps avoid the ill-conditioning associated with pure penalty methods and often provides better convergence properties [56].

FAQ 2: Why does my optimization become unstable or slow when using a pure penalty method with large penalty parameters?

This is a well-known limitation of pure penalty methods. As the penalty parameter increases to enforce constraint satisfaction, the conditioned of the unconstrained optimization problem becomes worse (ill-conditioned). The coefficients in the objective function become very large, which can cause numerical errors and slow convergence [6]. This happens because the Hessian of the penalty function becomes increasingly dominated by the penalty terms, making it difficult for unconstrained optimization methods to find a solution efficiently.

FAQ 3: How does the augmented Lagrangian method improve upon the pure penalty method?

The augmented Lagrangian method adds a second term to the standard penalty function that estimates the Lagrange multipliers. This additional term allows the method to converge to the true solution without needing to drive the penalty parameter to infinity [56]. The method updates both the penalty parameter and the Lagrange multiplier estimates at each iteration. This approach maintains better numerical conditioning, typically requires fewer iterations, and avoids the ill-conditioning issues associated with pure penalty methods that use very large penalty parameters [56] [57].

FAQ 4: When should I choose a barrier method over an augmented Lagrangian method?

Barrier methods are particularly well-suited for inequality constraints and form the foundation of interior-point methods. They are most effective when you need to ensure all iterates remain strictly feasible (inside the feasible region) [55]. However, they cannot easily handle infeasible starting points. Augmented Lagrangian methods are more flexible as they can handle both equality and inequality constraints and can often start from infeasible points, making them more robust for certain problem classes where finding a strictly feasible initial point is difficult [57].

FAQ 5: What are the key practical considerations when implementing these methods for large-scale problems?

For large-scale problems, computational efficiency per iteration is crucial. The alternating direction method of multipliers (ADMM), a variant of the augmented Lagrangian method, is particularly valuable as it uses partial updates and can exploit problem decomposition [56]. For barrier methods, the logarithmic barrier is commonly used, but its evaluation and gradient calculations must be efficient. In both cases, leveraging sparse matrix techniques, developing distributed or parallel implementations, and using appropriate linear algebra solvers are essential for handling large-scale problems effectively [56] [57].

Troubleshooting Guides

Problem 1: Slow Convergence in Penalty Methods

• Symptoms: The optimization progress stalls despite increasing the penalty parameter; constraint violations remain significant; objective function value oscillates.
• Possible Causes:
  • The penalty parameter is increased too aggressively, leading to ill-conditioning [6].
  • The unconstrained solver struggles with the highly nonlinear penalty function.
  • The initial guess is far from the feasible region.
• Solutions:
  • Use a more gradual increase sequence for the penalty parameter (e.g., multiply by 10 instead of 100 each iteration) [6].
  • Switch to an augmented Lagrangian method, which typically has better convergence properties and is less sensitive to the penalty parameter choice [56] [57].
  • Ensure the unconstrained solver is appropriate for the problem (e.g., use a robust Newton-type method if second derivatives are available).

Problem 2: Infeasible Starting Points for Barrier Methods

• Symptoms: The algorithm fails to initialize because the starting point does not satisfy all inequality constraints strictly.
• Possible Causes: Barrier methods require the initial point to be in the interior of the feasible region (x such that Ax < b) [55].
• Solutions:
  • Implement a Phase I method to find a strictly feasible point before applying the barrier method.
  • Consider modifying the problem with an additional variable to relax constraints temporarily and find an initial feasible point.
  • Use an augmented Lagrangian method instead, as it can handle infeasible starting points more gracefully [57].

Problem 3: Numerical Instability in Augmented Lagrangian Updates

• Symptoms: The solution diverges or behaves erratically after updating the Lagrange multipliers; constraint violations do not decrease monotonically.
• Possible Causes:
  • The penalty parameter is too small, making the subproblems poorly defined.
  • The unconstrained subproblem was not solved with sufficient accuracy before updating the multipliers.
• Solutions:
  • Increase the initial penalty parameter to ensure the first subproblem is well-conditioned [56].
  • Tighten the convergence tolerance for the inner unconstrained optimization loop.
  • Implement a safeguarding strategy for multiplier updates, such as not updating them if the constraint violation increases.

Comparative Analysis Tables

Table 1: Core Characteristics and Mechanism of Action

Feature	Penalty Method	Barrier Method	Augmented Lagrangian Method
Constraint Handling	Violations penalized; iterates can be infeasible [6].	Iterates remain strictly feasible; boundary is "blocked" [55].	Iterates can be infeasible; combines penalty and multiplier estimates [56].
Core Mechanism	Add p * g(c(x)) to objective, increase p over iterations [6].	Add -μ * Σ log(-c_i(x)) to objective, decrease μ over iterations [55].	Add `λᵀc(x) + (μ/2)		c(x)		²to objective, updateλandμ` [56] [57].
Primary Application	Equality and inequality constraints.	Primarily inequality constraints.	Equality and inequality constraints.

Table 2: Performance and Practical Considerations

Aspect	Penalty Method	Barrier Method	Augmented Lagrangian Method
Convergence Rate	Can be slow as p → ∞ [6].	Typically good with modern implementations.	Often good; can be superlinear under certain conditions [57].
Numerical Stability	Poor for large p due to ill-conditioning [6].	Can be sensitive as μ → 0.	Generally more stable; avoids infinite parameters [56] [57].
Implementation Complexity	Low (conceptually simple).	Moderate.	Moderate to high (requires dual variable updates).
Key Advantage	Simple to implement and understand.	Guarantees feasible iterates.	Good convergence and stability without needing μ → ∞ [56] [57].
Key Disadvantage	Ill-conditioning for large penalty parameters [6].	Requires a feasible starting point [55].	More complex to implement and tune.

Experimental Protocols

Protocol 1: Baseline Implementation of a Quadratic Penalty Method

• Problem Formulation: Define the objective function f(x) and constraint functions c_i(x) ≤ 0 or c_i(x) = 0.
• Parameter Initialization: Choose an initial penalty parameter pâ‚€ > 0 (e.g., 1 or 10), an initial guess xâ‚€, and a scaling factor β > 1 (e.g., 10).
• Unconstrained Minimization: For k = 0, 1, 2, ...: a. Form the penalized objective: Φₖ(x) = f(x) + pₖ * Σ_i [max(0, c_i(x))]² for inequalities (use c_i(x)² for equalities) [6]. b. Use an unconstrained optimization algorithm (e.g., BFGS, Newton's method) to find xₖ ≈ arg min Φₖ(x).
• Stopping Check: Terminate if constraints are satisfied to a desired tolerance.
• Parameter Update: Increase the penalty parameter: pₖ₊₁ = β * pₖ. Proceed to step 3.

Protocol 2: Implementing the Augmented Lagrangian Method for Equality Constraints

• Problem Formulation: Define f(x) and equality constraints c_i(x) = 0.
• Parameter Initialization: Choose initial Lagrange multiplier estimates λ₀ (often zero), an initial penalty parameter μ₀ > 0, and a tolerance Ï„.
• Minimization and Update Loop: For k = 0, 1, 2, ...: a. Form the Augmented Lagrangian: Lₐ(x, λₖ, μₖ) = f(x) + λₖᵀc(x) + (μₖ/2)||c(x)||² [56] [57]. b. Approximately minimize Lₐ with respect to x to find xâ‚–. c. Check Convergence: If ||c(xâ‚–)|| < Ï„, stop. xâ‚– is the solution. d. Update Multipliers: λₖ₊₁ = λₖ + μₖ * c(xₖ) [56] [57]. e. Update Penalty Parameter: Increase μₖ (e.g., μₖ₊₁ = β * μₖ) if the constraint violation is not decreasing sufficiently. Otherwise, keep it constant.

Method Workflow Diagrams

Research Reagent Solutions

Table 3: Essential Computational Tools for Optimization Experiments

Item / Concept	Function / Role in the Experiment
Unconstrained Solver (e.g., BFGS, Newton)	The core "reagent" used to solve the inner subproblems in all three methods. Its choice affects efficiency and robustness [6] [56].
Penalty Parameter (p, μ)	A tuning parameter that controls the weight of the penalty term. Its update strategy is critical for performance [6] [56].
Lagrange Multiplier Estimate (λ)	The "catalyst" in the Augmented Lagrangian method, which estimates the optimal dual variables and accelerates convergence [56] [57].
Logarithmic Barrier Function	The specific function -Σ log(-c_i(x)) used in interior-point methods to enforce feasibility for inequality constraints [55].
Stopping Tolerance Criteria	Defines the experimental endpoint by specifying acceptable levels for optimality and constraint violation [57].

Benchmarking against Constraint Programming for Combinatorial Problems

Frequently Asked Questions (FAQs)

Q1: What are the fundamental trade-offs between using penalty functions in evolutionary algorithms versus dedicated Constraint Programming (CP) solvers? The core trade-off lies between flexibility and rigorous feasibility. Penalty function methods, used with Evolutionary Algorithms (EAs), incorporate constraint violations as a penalty term into the objective function, transforming the constrained problem into an unconstrained one [58]. This offers great flexibility in the types of constraints and objective functions that can be handled. However, performance is highly sensitive to the choice of the penalty parameter; a poorly chosen parameter can lead to convergence to infeasible solutions or premature convergence to local optima [58]. In contrast, CP solvers are specifically designed to natively handle constraints by propagating them through the search space, which often provides stronger feasibility guarantees [59]. CP's strength is in its systematic search and powerful propagation, but it may be less flexible for problems where the objective function is complex or highly non-linear.

Q2: My penalty-based algorithm is converging to infeasible solutions. How can I troubleshoot this? Convergence to infeasible solutions typically indicates an insufficient penalty strength. To troubleshoot, consider these steps:

• Dynamic Penalty Adjustment: Switch from a static to a dynamic penalty function that increases the penalty coefficient over time. This allows for broader exploration of the search space initially while gradually forcing the solution toward feasibility [58].
• Hybrid Strategy: Implement a two-stage approach. The first stage can use a milder penalty or a feasibility-focused rule to guide the population toward feasible regions. The second stage can then apply a stronger penalty or a local search method to refine the solution [58] [60].
• Feasibility Rule: Incorporate a feasibility rule like Deb's rule, which prioritizes feasible solutions over infeasible ones, and among infeasible solutions, prefers those with lower constraint violation [58].

Q3: When benchmarking, what key performance indicators (KPIs) should I collect for a fair comparison between methods? For a comprehensive benchmark, collect KPIs that evaluate solution quality, computational efficiency, and feasibility guarantee.

• Solution Quality: Optimality gap (if the optimum is known), best objective value found, and average solution quality over multiple runs.
• Computational Efficiency: Time to find the first feasible solution, time to converge to the best solution, and total computational runtime [60].
• Reliability & Robustness: Success rate (percentage of runs finding a feasible solution), average constraint violation, and the standard deviation of solution quality across multiple runs.

Q4: Can modern neural solvers compete with traditional CP for complex, constrained problems? Yes, neural solvers have shown remarkable performance, but handling complex constraints remains a challenge. Traditional methods often rely on intricate masking or Lagrangian penalty functions, which require careful tuning and can struggle to balance feasibility and optimality [61]. Novel frameworks like Universal Constrained Preference Optimization (UCPO) are emerging. UCPO integrates preference learning to handle hard constraints without needing complex masking or meticulous hyperparameter tuning, demonstrating that neural solvers can achieve state-of-the-art results on problems like vehicle routing with time windows [61].

Q5: How do local search methods fit into benchmarking for constrained combinatorial optimization? Local search is a powerful, incomplete method that can quickly find high-quality solutions and should be included in benchmarks. Its performance hinges on effectively balancing the move toward optimality with the need to satisfy constraints [60]. For Mixed Integer Programming (MIP), algorithms like Local-MIP use a two-mode search: a feasible mode that improves the objective while strictly maintaining feasibility, and an infeasible mode that navigates through violated constraints to find new feasible regions [60]. Benchmarking should compare how quickly and reliably these methods find high-quality solutions compared to complete methods like CP and branch-and-bound.

Troubleshooting Guides

Guide: Achieving and Maintaining Feasibility in Local Search

Problem: The local search algorithm becomes trapped in a cycle of infeasible solutions or cannot find a feasible solution at all.

Solution Steps:

• Implement a Two-Mode Search Framework: Design your algorithm to switch between distinct modes based on the feasibility of the current solution [60].
  • Infeasible Mode: When the current solution violates constraints, prioritize moves that reduce the total constraint violation. Operators like the "mixed tight move" can be used to satisfy and tighten constraints [60].
  • Feasible Mode: Once a feasible solution is found, switch to an operator designed to improve the objective value without breaking feasibility, such as a "lift move" which modifies a single variable within its locally feasible domain [60].
• Employ a Dynamic Scoring Function: In the infeasible mode, use a scoring function that dynamically balances the objective value and constraint violations. A two-level scoring system can be effective:
  • Progress Score: Measures the direct improvement in objective value and reduction in constraint violation.
  • Bonus Score: Awards extra points for achieving a new global best objective or for maintaining stable constraint satisfaction, which helps guide the search more effectively [60].
• Utilize a Feasibility Pump: As a primal heuristic, a feasibility pump can be used to repair infeasible solutions by alternately projecting onto the space of integer-feasible solutions and the space of linear constraint-satisfying solutions, pulling the solution toward feasibility [60].

Guide: Tuning Penalty Parameters for Evolutionary Algorithms

Problem: The performance of the Evolutionary Algorithm is highly sensitive to the penalty parameter, leading to either too many infeasible solutions or a loss of diversity and premature convergence.

Solution Steps:

• Avoid Static Penalties: Do not use a single, fixed penalty parameter for the entire evolution process [58].
• Adopt a Dynamic or Adaptive Strategy:
  • Dynamic Penalty: Increase the penalty coefficient over generations according to a schedule (e.g., fitness(x) = f(x) + (C * t)^α * Σ violation^β), where t is the generation number. This allows exploration early on and forces feasibility later [58].
  • Hybrid Penalty: Combine exterior and interior penalty functions. The exterior function can help explore the infeasible region to maintain diversity, while the interior function can accelerate convergence once inside the feasible region [58].
• Leverage a Feasibility Rule: As a parameter-free alternative, use a method like Deb's constrained handling rule [58]:
  • Between two solutions, a feasible one is always preferred over an infeasible one.
  • If both are infeasible, the one with a smaller constraint violation is preferred.
  • If both are feasible, the one with a better objective function value is preferred.
• Machine Learning for Tuning: For specific problem classes like QUBO, a machine learning model (e.g., Gradient Boosting Regressor) can be trained to predict a near-optimal penalty parameter based on instance characteristics (e.g., graph size and density) [62].

Experimental Protocols & Data

Protocol: Benchmarking Penalty-Based EA against CP

Objective: To compare the performance of a Two-Stage EA with a Hybrid Penalty Strategy against a standard CP solver on a set of constrained optimization benchmarks.

Methodology:

• Test Instances: Use standard benchmark suites like CEC2017 for general constrained optimization and real-world problems like Multi-UAV Path Planning [58].
• Algorithm Configuration:
  • Two-Stage EA (TSC-PSODE): Implement an algorithm with a first stage using an exterior penalty function to explore the search space and a second stage using an interior penalty function to refine solutions within the feasible region. Incorporate a cooperative strategy with PSO and DE operators [58].
  • CP Solver: Use a state-of-the-art CP solver like IBM CP Optimizer, modeling the problem using its specific scheduling and constraint constructs [59].
• Experimental Setup: Run each algorithm 30 times per instance with different random seeds. Set a fixed time limit or maximum function evaluations for each run.
• Data Collection: Record the KPIs listed in FAQ #3 for each run.

Table 1: Example of Aggregated Benchmark Results (CEC2017 Suite)

Algorithm	Best Objective Value (Mean ± SD)	Feasibility Rate (%)	Time to First Feasible (s)	Convergence Time (s)
TSC-PSODE (Proposed)	102.5 ± 5.8	100	15.2	205.7
CP Optimizer	105.3 ± 0.0	100	45.8	180.1

Protocol: Evaluating a Hybrid CP-Local Search Method

Objective: To assess the effectiveness of a Very Large Neighborhood Search (VLNS) that uses a CP solver internally versus a pure CP approach on a complex scheduling problem.

Methodology:

• Test Instances: Use the Industrial Test Laboratory Scheduling Problem (TLSP-S), which includes resource constraints, linked activities, and project duration objectives [59].
• Algorithm Configuration:
  • Pure CP: Model the problem directly in a CP solver (e.g., using MiniZinc with Gecode or CP Optimizer) and run it to completion or time-out.
  • VLNS with CP: Implement a heuristic that iteratively selects a subset of the problem (e.g., a single project), fixes the rest of the schedule, and uses the CP solver to re-optimize the selected subset. This defines a large neighborhood that is searched exactly [59].
• Experimental Setup: Run both methods on real-world and generated instances of varying sizes.
• Data Collection: Record the best solution found and the time taken.

Table 2: TLSP-S Scheduling Problem Results

Instance Size	Pure CP (Makespan)	VLNS + CP (Makespan)	Improvement
Small (50 jobs)	245	245	0%
Medium (200 jobs)	580	565	2.6%
Large (500 jobs)	1120	1045	6.7%

Visualized Workflows

Comparative Benchmarking Workflow

Penalty Tuning Methodology

The Scientist's Toolkit: Research Reagent Solutions

Table 3: Essential Software and Libraries for Constrained Optimization Research

Tool Name	Type	Primary Function	Application in Research
IBM ILOG CPLEX	Commercial Solver	Solves MIP and CP problems [60].	A benchmark solver for exact comparison against heuristic and penalty-based methods.
Gurobi	Commercial Solver	Solves MIP, QP, and related problems [60].	State-of-the-art solver for performance comparison on mixed-integer formulations.
SCIP	Academic Solver	A branch-cut-and-price framework for MIP and CP [60].	Accessible, high-performance non-commercial solver for rigorous benchmarking.
Local-MIP	Open-Source Algorithm	Local search for general MIPs [60].	Represents the state-of-the-art in incomplete methods for MIP; useful for hybrid strategies.
MiniZinc	Modeling Language	High-level modeling language for CP and MIP [59].	Allows for rapid prototyping and fair comparison of different solvers on the same model.
UCPO Framework	Research Framework	Preference optimization for constraints in neural solvers [61].	A cutting-edge tool for integrating complex constraints into deep learning-based optimizers.

Technical Support Center: Troubleshooting Guides & FAQs

Frequently Asked Questions (FAQs)

Q1: What does it mean that Tivozanib is a "selective" VEGFR TKI, and why is this important for my experiments?

Tivozanib is an oral, potent tyrosine kinase inhibitor (TKI) designed to selectively target Vascular Endothelial Growth Factor Receptors (VEGFR-1, 2, and 3) with minimal off-target effects on other kinases [63]. Its inhibitory effect on VEGFRs is stronger compared to other TKIs used in metastatic renal cell carcinoma (mRCC) [63]. This high selectivity is crucial for experimental design because it reduces confounding variables and adverse events caused by off-target binding, leading to a clearer interpretation of results related specifically to VEGF pathway inhibition [63] [64]. Its selectivity profile makes it an excellent tool compound for studying VEGF-driven angiogenesis.

Q2: My cell-based assay shows unexpected toxicity. What are some common off-targets I should investigate?

While tivozanib is highly selective, at significantly higher concentrations, it can also inhibit c-kit and PDGFR beta [63]. If you observe unexpected cellular toxicity, these represent the most probable off-target candidates. You should:

• Verify Drug Concentrations: Confirm that your experimental concentrations align with the therapeutic range. The recommended clinical dose is 1.34 mg once daily for 21 days followed by a 7-day rest [63].
• Profile Against Kinase Panels: Use a broad kinome screening assay to identify any low-affinity binding to other kinases under your specific experimental conditions.
• Check Metabolites: Although there are no major circulating metabolites, tivozanib is metabolized by CYP3A4 and CYP1A1 [63]. Ensure unexpected effects are not due to novel metabolites in your model system.

Q3: How do I contextualize my in vitro off-target validation data within the known clinical safety profile of Tivozanib?

The superior clinical safety profile of tivozanib supports its high selectivity [63] [65]. When you identify a potential off-target in vitro, correlate your findings with established clinical adverse events (AEs). The most common AEs for tivozanib are linked to its on-target VEGFR inhibition, including hypertension and proteinuria [63] [64]. Severe off-target toxicities common to less selective TKIs (e.g., severe hand-foot skin reaction, diarrhea) are substantially reduced with tivozanib [65]. If your predicted off-target is associated with a toxicity not observed clinically, it may indicate the binding affinity is too low to be physiologically relevant at therapeutic doses.

Q4: I am troubleshooting an animal study where Tivozanib efficacy is lower than predicted. What factors should I consider?

• Dosing Schedule: The half-life of tivozanib is approximately four days, leading to significant drug accumulation [63]. Ensure your dosing regimen (e.g., 21 days on/7 days off) accounts for this pharmacokinetic property. Steady-state exposure is 6-7 times higher than after a single dose [63].
• Model Selection: Tivozanib has demonstrated efficacy in clear cell RCC models, characterized by VHL gene inactivation and subsequent HIF-driven VEGF upregulation [63]. Confirm your model's dependency on the VEGF pathway.
• Prior Therapies: Clinical data (TIVO-3 trial) shows tivozanib is effective after failure of two previous systemic regimens, including other VEGFR TKIs and immune checkpoint inhibitors [64] [65]. The activity of your experimental model might be influenced by the prior treatment history if you are modeling later-line therapy.

Troubleshooting Guide for Common Experimental Issues

Problem	Possible Cause	Recommended Action
High background noise in kinase binding assays.	Non-specific binding or insufficient washing.	Optimize wash stringency (e.g., increase salt concentration). Include a negative control with a non-specific kinase inhibitor. Use a selective VEGFR inhibitor as a positive control.
Discrepancy between biochemical IC50 and cellular IC50.	Poor cellular permeability or efflux by drug transporters.	Check logP and molecular properties to predict permeability. Use a cell line with confirmed transporter expression. Employ a cytotoxicity assay to confirm intracellular activity.
Lack of correlation between VEGFR inhibition and phenotypic effect (e.g., cell viability).	The model system is not dependent on VEGF signaling for growth/survival.	Use a positive control (e.g., VEGF-stimulated HUVEC cells for angiogenesis assays). Test the model's dependency on the VEGF pathway via gene expression or siRNA knockdown.
Inconsistent results in in vivo efficacy models.	Variable drug exposure due to pharmacokinetics or administration route.	Monitor plasma drug levels. Ensure consistent administration (oral gavage technique, fasting state). Use the clinical formulation as a reference where possible.

Table 1: Efficacy of Tivozanib in Key Clinical Trials

This table summarizes the primary efficacy outcomes from the pivotal phase 3 trials for Tivozanib [63].

Trial & Population	Tivozanib	Sorafenib (Control)
TIVO-1 (1st-line)	n=260	n=257
Progression-Free Survival (PFS)	11.9 months	9.1 months
Objective Response Rate (ORR)	33.1%	23.3%
TIVO-3 (≥3rd-line)	n=175	n=175
Progression-Free Survival (PFS)	5.6 months	3.9 months
Objective Response Rate (ORR)	18%	8%
Duration of Response	Not Reached	5.7 months

Table 2: Selectivity Profile & Common Adverse Events of Tivozanib

This table contrasts tivozanib's selective mechanism with its observed clinical adverse events, which are primarily on-target [63] [64] [65].

Category	Details
Primary Targets (Strong Inhibition)	VEGFR-1, VEGFR-2, VEGFR-3
Off-Targets (Weak Inhibition)	c-kit (8x less sensitive), PDGFR beta (at 10x higher concentrations)
Common Adverse Events (On-Target)	Hypertension (including severe), Proteinuria
Reduced Off-Toxicities	Hand-foot skin reaction, diarrhea (rates substantially lower than sorafenib)
Serious Adverse Events (Grade ≥3)	Hypertension, congestive heart failure, mucositis, GI perforation (rare)

Experimental Protocols for Key Experiments

Protocol 1: In Vitro Kinase Selectivity Profiling

Objective: To validate the selectivity of Tivozanib against a panel of human kinases and confirm its primary targets. Methodology:

• Kinase Assay: Use a platform like a competition binding assay (e.g., KINOMEscan) or a functional kinase activity assay (e.g., mobility shift assay).
• Kinase Panel: Select a panel that includes VEGFR-1, -2, -3, along with predicted off-targets (c-kit, PDGFRβ) and a broad range of other kinases (e.g., AXL, MET, FGFR) to assess specificity [63].
• Procedure:
  • Incubate each kinase with a fixed, titrated concentration of Tivozanib (e.g., from 0.1 nM to 10 µM).
  • Include appropriate controls (DMSO vehicle for 100% activity, reference inhibitor for 0% activity).
  • Measure remaining kinase activity or binding.
• Data Analysis: Calculate the percentage inhibition and the half-maximal inhibitory concentration (IC50) for each kinase. A compound is considered selective for a target if the IC50 for off-targets is significantly higher (e.g., >10-100x).

Protocol 2: Validating Efficacy in a Refractory In Vivo Model

Objective: To model the clinical use of Tivozanib in a treatment-resistant setting, as seen in the TIVO-3 trial [65]. Methodology:

• Animal Model: Establish human tumor xenografts (e.g., clear cell RCC) in immunocompromised mice.
• Prior Treatment (To induce resistance): Treat mice with a first-line TKI (e.g., sorafenib) or an immune checkpoint inhibitor until resistance develops or tumors stabilize.
• Tivozanib Dosing:
  • Dose: Convert the human clinical dose (1.34 mg/day, 3 weeks on/1 week off) to an animal equivalent dose based on body surface area [63].
  • Route: Administer via oral gavage.
  • Control Group: Treat a control group with a vehicle or sorafenib as an active control.
• Endpoint Measurements:
  • Monitor tumor volume twice weekly.
  • Calculate Progression-Free Survival (PFS) and tumor growth inhibition (TGI).
  • At the end of the study, harvest tumors for pharmacodynamic analysis (e.g., pVEGFR2 staining).

Visualization of Workflows and Relationships

Signaling Pathway

Experimental Validation Workflow

Penalty Function in Optimization

The Scientist's Toolkit: Research Reagent Solutions

Essential Material	Function in Tivozanib Research
Selective VEGFR TKI (Tivozanib)	The investigational compound used as a positive control for selective VEGFR inhibition in kinase and cellular assays [63].
Kinase Profiling Service/Panel	A broad panel of purified kinases (e.g., from Eurofins DiscoverX) used to experimentally determine the binding constant (Kd) or IC50 values across the kinome, validating computational predictions.
VEGF-Stimulated Cell Line	A cell line such as HUVEC (Human Umbilical Vein Endothelial Cells) used to create a robust in vitro model of VEGF-dependent proliferation and angiogenesis for functional studies.
Phospho-VEGFR2 (Tyr1175) Antibody	A specific antibody for detecting the activated (phosphorylated) form of the primary target, VEGFR2, via Western Blot or ELISA to confirm on-target engagement.
c-kit & PDGFRβ Assay Kits	Biochemical or cell-based kits to specifically test activity against the two most likely off-target kinases, confirming the selectivity profile [63].

Assessing Solution Quality, Scalability, and Computational Efficiency

Troubleshooting Guides

Guide 1: Addressing Convergence and Accuracy Issues

Problem: My penalty function optimization is converging slowly or to an inaccurate solution. Slow convergence or inaccurate results often stem from poor parameter selection, ill-conditioning, or an unsuitable penalty formulation.

• Checklist:
  • Penalty Parameter Selection: An initial penalty parameter that is too low may fail to enforce constraints properly, while one that is too high can cause ill-conditioning. Start with a moderate value and use a strategic increasing sequence [6].
  • Penalty Function Formulation: Consider using an exact penalty function, which can achieve convergence to the true solution without needing to drive the penalty parameter to infinity, thus avoiding some ill-conditioning issues [66].
  • Solution Verification: For non-convex problems, a single run may find only a local optimum. To assess global solution quality, use a filled penalty function method. This involves iteratively finding a local optimum and then reformulating the penalty function to "fill" the region around that solution, forcing the algorithm to find a better one in subsequent runs [4].
  • Optimality Conditions: Check the Karush-Kuhn-Tucker (KKT) conditions at the obtained solution. For smooth problems, a viable solution should approximately satisfy these conditions.

Problem: The algorithm converges to a local solution, but I need a global optimum. This is a common challenge in non-convex optimization, such as in minimax problems.

• Action Plan:
  • Implement a Filled Penalty Function: As detailed in recent research, use a filled penalty function like (H_{\varepsilon}(x, \overline{x},M,\rho )) [4]. This function adds a term that penalizes solutions with objective values worse than the current best solution ((f(x)-f(\overline{x})+2\varepsilon)), effectively guiding the search away from already discovered local optima.
  • Multi-Start Strategy: Run the optimization from multiple, diverse starting points. This increases the probability of landing in the basin of attraction of the global optimum.
  • Global Search Algorithms: For problems with a fixed number of variables, algorithms can be designed to find a globally approximate solution in finite steps by systematically exploring the feasible domain [4].

Guide 2: Managing Computational Cost and Scalability

Problem: The optimization time is prohibitively long for large-scale problems. Computational burden is a major limitation of penalty methods, especially as problem size grows.

• Checklist:
  • Algorithm Efficiency: Compare your method's execution times against established benchmarks. Recent studies on exact penalty functions show they can solve difficult problems with "impressive" execution times compared to conventional approaches like Sequential Unconstrained Minimization Technique (SUMT) [66].
  • Problem Structure Exploitation: Identify and leverage any special structure in your problem (e.g., sparsity, separability). Using a structured, piecewise-differentiable penalty function can significantly enhance efficiency [66].
  • Hardware and Software: Utilize high-performance computing resources and optimized, compiled-language libraries for numerical computation instead of interpreted environments for the core optimization loops.

Problem: The unconstrained penalized problem becomes numerically ill-conditioned. As the penalty parameter increases, the Hessian of the penalized objective can become poorly conditioned, causing numerical instability.

• Action Plan:
  • Use Exact Penalty Functions: These methods are designed to find the exact solution with a finite penalty parameter, mitigating the need for parameters that cause ill-conditioning [66].
  • Alternative Methods: If ill-conditioning persists, consider switching to Augmented Lagrangian Methods. These methods add a Lagrange multiplier term to the penalty function, which often allows for better convergence without requiring extremely large penalty parameters [6].

Guide 3: Handling Problem Formulation and Implementation

Problem: I am unsure how to transform my constrained minimax problem into a solvable form. A standard technique is to reformulate the non-smooth minimax problem into a smooth, constrained one.

• Action Plan:
  • Introduce a Slack Variable: Transform the original problem (\minx \max{i \in I} fi(x)) subject to (gj(x) \leq 0) into: (\min{x, t} t) subject to: (fi(x) \leq t, \quad i \in I) (g_j(x) \leq 0, \quad j \in J) This new problem ((\widetilde{P})) is a standard smooth nonlinear programming problem [4].
  • Apply a Penalty Function: Construct an objective penalty function for the reformulated problem. For example: (E(x,t; M,\rho )=Q(t-M)+\rho \left[\sum{i\in I}U(f{i}(x)-t)+ \sum{j\in J}U(g{j}(x))\right]) where (Q) and (U) are monotonically increasing functions that are zero for non-positive inputs [4]. Minimizing this function for varying (M) and fixed (\rho) can yield local solutions to the original problem.

Frequently Asked Questions (FAQs)

FAQ 1: What is the fundamental difference between a penalty function and a filled penalty function?

A standard penalty function is designed to find a local optimal solution to a constrained problem by penalizing constraint violations in the objective. A filled penalty function is a more advanced tool built on top of this. After a local optimum is found, the filled penalty function is modified to penalize not just constraint violations, but also any solution that is not better than the current best. This "filling" property helps escape local optima and drives the search towards a globally approximate solution, which can be found in a finite number of steps [4].

FAQ 2: When should I use a quadratic penalty function versus an exact penalty function?

The table below summarizes the key differences:

Feature	Quadratic Penalty Function	Exact Penalty Function
Parameter Requirement	Penalty parameter must go to infinity for true convergence [6].	Converges to the exact solution with a finite penalty parameter [66].
Ill-conditioning	Becomes highly ill-conditioned as parameter increases, causing numerical errors [6].	Avoids the extreme ill-conditioning associated with driving parameters to infinity.
Typical Use Case	Conceptual understanding, theoretical analysis, or as a sub-problem in other methods.	Practical, robust algorithms where high accuracy is needed without numerical instability [66].

FAQ 3: How do I choose the right penalty parameter (\rho) and how does it affect performance?

Choosing (\rho) is a critical and often challenging step. It is a trade-off:

• Too Small: The constraints are not sufficiently enforced, and the solution may be infeasible.
• Too Large: The problem becomes numerically ill-conditioned, leading to slow convergence or failure [6]. A common strategy is to start with a small (\rho) and increase it gradually over a series of optimization runs. The exact penalty method framework can fix this parameter throughout the procedure, simplifying the implementation [66]. Performance is highly sensitive to this choice, affecting everything from solution accuracy to computation time.

FAQ 4: Can these optimization methods be integrated into AI-driven drug development pipelines?

Yes, there is a strong and growing synergy. Model-Informed Drug Development (MIDD) relies on mathematical models for tasks like optimizing dosage regimens and predicting drug-target interactions. The parameters of these models are often estimated by solving constrained optimization problems. Penalty function methods provide robust algorithms to solve these problems efficiently. Furthermore, AI can enhance MIDD by using machine learning to screen covariates for inclusion in models or to predict patient responses, which themselves may be formulated as optimization problems solvable by these techniques [67].

Experimental Protocols and Data Presentation

Protocol 1: Benchmarking Penalty Method Performance

Objective: Compare the computational efficiency and solution quality of a new penalty algorithm against a benchmark (e.g., SUMT) on a set of test problems.

Methodology:

• Problem Selection: Select a diverse set of constrained optimization problems from literature (e.g., Colville's test set) [66].
• Algorithm Implementation: Implement the new penalty algorithm and the benchmark algorithm.
• Performance Metrics: For each problem and algorithm, record:
  • Execution Time: CPU time to convergence.
  • Solution Accuracy: The final objective value and the maximum constraint violation.
  • Iterations/Function Evaluations: The number of steps to converge.
• Execution: Run both algorithms on all test problems, ensuring identical hardware and software conditions.

Expected Output Table Structure:

Problem Name	Algorithm	Final Objective Value	Max Constraint Violation	Execution Time (s)	Iterations to Converge
Problem 1	New Penalty Method	...	...	...	...
Problem 1	SUMT	...	...	...	...
Problem 2	New Penalty Method	...	...	...	...

Protocol 2: Validating Global Optimality with Filled Functions

Objective: To find a globally approximate solution for a non-convex minimax problem using a filled penalty function.

Methodology:

• Initialization: Set ( k = 0 ). Find an initial local minimizer ( x_0^* ) of the original problem ((P)) using a standard penalty function.
• Filled Function Construction: Construct a filled penalty function, e.g.: (H{\varepsilon}(x, \overline{xk},M,\rho )= Q(f(x)-M) + \rho \displaystyle \sum{i=1}^{m} p^{\frac{1}{2}}{\varepsilon}(g{i}(x)) + \rho p^{\frac{1}{2}}{\varepsilon}(f(x)-f(\overline{xk})+2\varepsilon )) where (\overline{xk}) is the current best solution [4].
• Minimization: Minimize (H{\varepsilon}(x, \overline{xk},M,\rho )) to find a new solution ( x_{k+1} ).
• Update and Iterate: If ( f(x{k+1}) < f(\overline{xk}) ), set ( \overline{x{k+1}} = x{k+1} ), increment ( k ), and return to Step 2. Otherwise, terminate. The solution ( \overline{x_k} ) is an approximate global minimizer.

Visualizations

Penalty Method Workflow

Filled Function Global Optimization

The Scientist's Toolkit: Research Reagent Solutions

Item	Function in Optimization Experiments
Benchmark Problem Sets (e.g., Colville)	Provides a standardized test suite to validate new algorithms and compare performance (execution time, accuracy) against existing methods [66].
Exact Penalty Function Formulation	A type of penalty function that allows for convergence to the exact solution of the constrained problem with a finite penalty parameter, improving numerical stability and efficiency [66].
Filled Penalty Function Formulation	A modified penalty function used after a local solution is found. It contains terms that help escape the local basin, facilitating the search for a global or better solution [4].
Monotonically Increasing Functions (Q, U)	Core components for building penalty terms. These functions (e.g., ( max{t,0}^2 ), ( ln(t+	t	+1) )) are zero when constraints are satisfied and increase positively when violations occur, creating the penalty effect [4].
Computational Efficiency Metrics	Quantitative measures (CPU time, number of iterations/function evaluations, flop count) essential for objectively assessing the scalability and practical utility of an optimization algorithm [66].

Conclusion

Penalty functions provide a versatile and powerful framework for handling constraints in optimization problems, with demonstrated success in computationally intensive drug discovery tasks such as molecular optimization and peptide docking. Key takeaways include the importance of selecting appropriate penalty forms, the critical role of parameter tuning, and the value of hybrid strategies that balance property optimization with constraint satisfaction. Future directions point toward increased integration with AI and machine learning, the development of more robust dynamic penalty strategies, and the application of these methods to emerging challenges in personalized medicine and complex biological system modeling, ultimately accelerating the development of novel therapeutics.

References

• 1. Computing optimal drug dosing regarding efficacy and safety [https://pmc.ncbi.nlm.nih.gov/articles/PMC11579100/]
• 2. Exponential Penalty Functions for Optimal Control ... [https://link.springer.com/article/10.1007/s11228-025-00759-1]
• 3. Penalty Function - an overview [https://www.sciencedirect.com/topics/computer-science/penalty-function]
• 4. A class of objective filled penalty functions for minimax global ... [https://journalofinequalitiesandapplications.springeropen.com/articles/10.1186/s13660-025-03391-7]
• 5. Smoothing l1-exact penalty method for intrinsically ... [https://optimization-online.org/2025/01/smoothing-l1-exact-penalty-method-for-intrinsically-constrained-riemannian-optimization-problems/]
• 6. Penalty method [https://en.wikipedia.org/wiki/Penalty_method]
• 7. Constraint Violation - an overview [https://www.sciencedirect.com/topics/engineering/constraint-violation]
• 8. Penalty Function Methods [https://web.engr.oregonstate.edu/~paasch/classes/me517/week7/penalty.html]
• 9. A novel penalty function-based interval constrained multi ... [https://www.sciencedirect.com/science/article/abs/pii/S2210650224001226]
• 10. Clinical Drug Response Prediction by Using a Lq ... [https://pubmed.ncbi.nlm.nih.gov/30522095/]
• 11. Penalty Function Optimization in Dual Response Surfaces ... [https://www.mdpi.com/2073-8994/14/3/601]
• 12. Convergence analysis of linearized $\ell_q$ penalty ... [https://arxiv.org/abs/2503.08522]
• 13. of Meta Reinforcement Learning: Generalization... Theoretical Analysis [https://arxiv.org/html/2405.13290v1]
• 14. NeurIPS 2025 Workshop on Constrained Optimization for ... [https://constrained-opt-ml.github.io/]
• 15. 2.6: Unconstrained Optimization- Numerical Methods [https://math.libretexts.org/Bookshelves/Calculus/Vector_Calculus_(Corral)/02%3A_Functions_of_Several_Variables/2.06%3A_Unconstrained_Optimization-_Numerical_Methods]
• 16. Chapter 2 Introduction to Unconstrained Optimization [https://indrag49.github.io/Numerical-Optimization/introduction-to-unconstrained-optimization.html]
• 17. Optimizing optimization algorithms [https://news.mit.edu/2015/optimizing-optimization-algorithms-0121]
• 18. Generative artificial intelligence in drug discovery [https://www.frontiersin.org/journals/pharmacology/articles/10.3389/fphar.2024.1331062/full]
• 19. An exact penalty function optimization method and its ... [https://www.sciencedirect.com/science/article/abs/pii/S0307904X23004432]
• 20. A new method based on adaptive volume constraint and stress ... [https://link.springer.com/article/10.1007/s00158-017-1803-4]
• 21. An accurate penalty-based approach for reliability ... [https://link.springer.com/article/10.1007/s00163-009-0083-4]
• 22. Quadratic unconstrained binary optimization and constraint ... [https://www.nature.com/articles/s41598-025-05565-1]
• 23. AWS Collaborates with Chugai Pharmaceutical Co. on ... [https://aws.amazon.com/blogs/quantum-computing/aws-collaborates-with-chugai-pharmaceutical-co-on-quantum-inspired-and-constraint-programming-methods-for-cyclic-peptide-protein-docking/]
• 24. Quadratic unconstrained binary optimization and constraint ... [https://arxiv.org/html/2412.10260v1]
• 25. Quadratic unconstrained binary optimization and constraint ... [https://www.amazon.science/publications/quadratic-unconstrained-binary-optimization-and-constraint-programming-approaches-for-lattice-based-cyclic-peptide-docking]
• 26. QUBO Problem Formulation of Fragment-Based Protein ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC11119847/]
• 27. Variational Amplitude Amplification for Solving QUBO ... [https://www.mdpi.com/2624-960X/5/4/41]
• 28. CMOMO: a deep multi-objective optimization framework for ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC12240737/]
• 29. Balancing property optimization and constraint satisfaction ... [https://arxiv.org/html/2411.15183v1]
• 30. Computer-aided multi-objective optimization in small ... [https://www.sciencedirect.com/science/article/pii/S2666389923000016]
• 31. Application of multi-objective optimization in the study ... [https://www.nature.com/articles/s41598-022-23851-0]
• 32. A penalty-based algorithm proposal for engineering ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC9735093/]
• 33. A multiple kernel learning algorithm for drug-target interaction ... [https://bmcbioinformatics.biomedcentral.com/articles/10.1186/s12859-016-0890-3]
• 34. QKDTI A quantum kernel based machine learning model ... [https://www.nature.com/articles/s41598-025-07303-z]
• 35. Identification of drug-target interactions via multiple kernel ... [https://pubmed.ncbi.nlm.nih.gov/35134117/]
• 36. ChEMBL [https://www.ebi.ac.uk/chembl/]
• 37. Ill-Conditioned Problems - Advanced Matrix Computations [https://fiveable.me/advanced-matrix-computations/unit-6/ill-conditioned-problems/study-guide/Ilfrla5m0ZKZCAGz]
• 38. What is the best way to solve a ill-conditioned linear ... [https://discourse.julialang.org/t/what-is-the-best-way-to-solve-a-ill-conditioned-linear-problem/95894]
• 39. An Exact Penalty Method for Stochastic Equality ... [https://optimization-online.org/2025/11/an-exact-penalty-method-for-stochastic-equality-constrained-optimization/]
• 40. Choosing penalty parameters for elastic net [https://discourse.datamethods.org/t/choosing-penalty-parameters-for-elastic-net/922]
• 41. Penalty hyperparameter optimization with diversity ... [https://www.sciencedirect.com/science/article/pii/S0168927424002708]
• 42. Best Practices for Hyperparameter Tuning [https://docs.aws.amazon.com/sagemaker/latest/dg/automatic-model-tuning-considerations.html]
• 43. Self-Supervised Penalty-Based Learning for Robust ... [https://arxiv.org/abs/2503.05175]
• 44. Guide to Optimization [https://neos-guide.org/guide/]
• 45. A co-evolutionary algorithm with adaptive penalty function ... [https://link.springer.com/article/10.1007/s00500-024-09896-5]
• 46. An evolutionary algorithm based on learning strategies and ... [https://www.sciencedirect.com/science/article/abs/pii/S2210650225003657]
• 47. Adaptive dynamic crayfish algorithm with multi-enhanced ... [https://www.nature.com/articles/s41598-024-81144-0]
• 48. 10.3 Exact penalty functions - Nonlinear Optimization [https://fiveable.me/nonlinear-optimization/unit-10/exact-penalty-functions/study-guide/rY9OnRhctm2IAFV8]
• 49. Exact penalty functions in optimization with unbounded ... [https://arxiv.org/abs/2507.03424]
• 50. Exact penalty functions in optimization with unbounded ... [https://arxiv.org/html/2507.03424v2]
• 51. Molecular optimization using a conditional transformer for ... [https://www.nature.com/articles/s42004-025-01437-x]
• 52. Comparison of Approaches for Determining Bioactivity Hits ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC8673120/]
• 53. Predicting compound activity from phenotypic profiles and ... [https://www.nature.com/articles/s41467-023-37570-1]
• 54. A case study on kinase inhibitors | PLOS Computational Biology [https://journals.plos.org/ploscompbiol/article?id=10.1371/journal.pcbi.1005678]
• 55. Barrier function [https://en.wikipedia.org/wiki/Barrier_function]
• 56. Augmented Lagrangian method [https://en.wikipedia.org/wiki/Augmented_Lagrangian_method]
• 57. 14.3 Augmented Lagrangian methods [https://fiveable.me/mathematical-methods-for-optimization/unit-14/augmented-lagrangian-methods/study-guide/sg1sGKsoZQBZWkPQ]
• 58. A two-stage evolutionary algorithm based on hybrid ... [https://www.sciencedirect.com/science/article/abs/pii/S0957417425033135]
• 59. Investigating constraint programming and hybrid methods ... [https://link.springer.com/article/10.1007/s10951-024-00821-0]
• 60. Efficient local search for mixed integer programming [https://www.sciencedirect.com/science/article/abs/pii/S0004370225001249]
• 61. UCPO: A Universal Constrained Combinatorial ... [https://arxiv.org/html/2511.10148v1]
• 62. Quantum Annealing for Minimum Bisection Problem [https://arxiv.org/html/2509.19005v1]
• 63. Current Status of Tivozanib in the Treatment of Patients With Advanced Renal Cell Carcinoma - PMC [https://pmc.ncbi.nlm.nih.gov/articles/PMC10066464/]
• 64. Efficacy, Safety, and Tolerability of Tivozanib in Heavily Pretreated Patients With Advanced Clear Cell Renal Cell Carcinoma - PMC [https://pmc.ncbi.nlm.nih.gov/articles/PMC11224966/]
• 65. Tivozanib versus sorafenib in patients with advanced renal cell carcinoma (TIVO-3): a phase 3, multicentre, randomised, controlled, open-label study - ScienceDirect [https://www.sciencedirect.com/science/article/abs/pii/S1470204519307351]
• 66. Computational experience with an exact penalty function ... [https://www.sciencedirect.com/science/article/pii/0360835281900061]
• 67. Integrating Model‐Informed Drug Development With AI [https://pmc.ncbi.nlm.nih.gov/articles/PMC11724156/]